题目内容
在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱。
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
(1)0.05(2)0.45(3)1200
解析试题分析:把3只黄色乒乓球标记为A、B、C,3只白色的乒乓球标记为1、2、3。
从6个球中随机摸出3个的基本事件为:ABC、AB1、AB2、AB3、AC1、AC2、AC3、A12、A13、A23、BC1、BC2、BC3、B12、B13、B23、C12、C13、C23、123,共20个
(1)事件E={摸出的3个球为白球},事件E包含的基本事件有1个,即摸出123号3个球,P(E)="1/20=0.05" 4分
(2)事件F={摸出的3个球为2个黄球1个白球},事件F包含的基本事件有9个,P(F)=9/20=0.45 8分
(3) 事件G={摸出的3个球为同一颜色}={摸出的3个球为白球或摸出的3个球为黄球},P(G)=2/20=0.1,假定一天中有100人次摸奖,由摸出的3个球为同一颜色的概率可估计事件G发生有10次,不发生90次。则一天可赚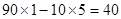 ,每月可赚1200元。 12分
,每月可赚1200元。 12分
考点:古典概型概率及期望
点评:古典概型概率的求解一般要首先找到所有的基本事件种数与满足题意的基本事件种数,求其比值即可,第三问是期望的简单应用

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案为了对某课题进行研究,用分层抽样的方法从 三所高校的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
三所高校的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人).
| 高校 | 相关人数 | 抽取人数 |
 | 18 |  |
 | 36 |  |
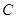 | 54 |  |
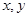 ;
;(2) 若从高校
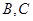 抽取的人中选2人作专题发言,求这2人都来自高校
抽取的人中选2人作专题发言,求这2人都来自高校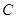 的概率.
的概率. 某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.
(Ⅰ)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(Ⅱ)花店记录了100 天玫瑰花的日需求量(单位:枝),整理得下表:
| 日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
(ii)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.
某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下表:
| 日销售量(吨) | 1 | 1.5 | 2 |
| 天数 | 10 | 25 | 15 |
(2)若以频率为概率,且每天的销售量相互独立.
①求5天中该种商品恰有2天的销售量为1.5吨的概率;
②已知每吨该商品的销售利润为2万元,X表示该种商品两天销售利润的和,求X的分布列和数学期望.
下表是我国2010年和2011年2~6月CPI同比(即当年某月与前一年同月相比)的增长数据,其中2011年的5个CPI数据成等差数列.
(Ⅰ)求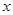 、
、 、
、 的值;
的值;
(Ⅱ)求2011年2~6月我国CPI数据的方差;
(Ⅲ)一般认为,某月CPI数据达到或超过3个百分点就已经通货膨胀,而达到或超过5个百分点为严重通货膨胀,现随机从2010年5个月和2011年5个月的数据中各抽取一个数据,求相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率.
我国2010年和2011年2~6月份的CPI数据(单位:百分点,1个百分点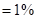 )
)
| 年份 | 二月 | 三月 | 四月 | 五月 | 六月 |
| 2010 | 2.7 | 2.4 | 2.8 | 3.1 | 3.9 |
| 2011 | 4.9 | 5.0 | 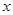 |  |  |
 )获得身高数据的茎叶图如下:
)获得身高数据的茎叶图如下: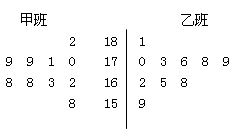
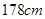 的同学,求至少有一名身高大于
的同学,求至少有一名身高大于 的同学被抽中的概率。
的同学被抽中的概率。 ,审核过关后,甲、乙两人文化测试合格的概率分别为
,审核过关后,甲、乙两人文化测试合格的概率分别为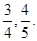
 表示甲,乙两人中获得自主招生入选资格的人数,求
表示甲,乙两人中获得自主招生入选资格的人数,求