Question

【题目】为了迎接2000年的到来，某地组织了一次乒乓球迎春幸运赛.首先，通过身份号抽选出2000名选手，编号为1，2，…，2000，他们当中任两人都可以组成一对双打选手，每对选手的编号之和称为他们的“和号”.规定：“和号”相同的两对选手方有资格进行幸运双打赛.比赛开始前，组委会首先从2000个编号中随机抽出65名幸运选手，然后找出“和号”相同的两对选手进行幸运双打赛（凡同一“和号”的选手分在同一区进行单循环）.求证：无论怎样抽选，总有选手进行幸运赛.

Answer 1

【答案】见解析

【解析】

因从1~2000两两作差（这里规定大数减小数），只有从1～1999共1999个数（作l999个抽屉）.

而任取65个编号(规定)两两作差（大数减小数），可得个差（作2080个苹果）.

由抽屉原理知，必存在差相等的情况.下面就差相等的个数进行讨论.

(1)若2080个差中，存在3个差相等的情况.设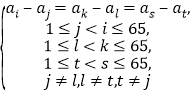

(i)若，则与配对，与配对，可进行幸运赛.

(ii)若（称为相邻等差对），则，从而与配对，与配对，可进行幸运赛.

(2)若2080个差中，不存在有3个差相等的情况，此时，由知，两个差相等的情况至少发生了81次.

考虑这些相等差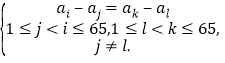：①

(i)若的情况不超过64次，则81个棚等差中必存在，使式①成立.此时与，配对，与配对，可进行幸运赛.

(ii)若的情况至少发生64次，由于此时的只能取共63个值，故必有关于的相邻等差对重复出现.即存在，使

相减得.

即与配对，与配对，可进行幸运赛.

综上得，随机抽出65名选手，总可进行幸运赛.