题目内容
20. 如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.
如图,已知正四棱柱ABCD-A1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.(1)求证:A1C⊥平面BDE;
(2)求BC与平面BDE所成角的正弦值.
分析 (1)首先分别以DA,DC,DD1三直线为x,y,z轴,建立空间直角坐标系,并求出一些点的坐标,设E(0,2,z),由BE⊥B1C即可求出z=1.可设平面BDE的法向量为$\overrightarrow{n}=(x,y,z)$,根据$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DE}=0}\\{\overrightarrow{n}•\overrightarrow{DB}=0}\end{array}\right.$即可求出法向量$\overrightarrow{n}$,从而可说明$\overrightarrow{{A}_{1}C}$∥$\overrightarrow{n}$,这样便得出A1C⊥平面BDE;
(2)求出向量$\overrightarrow{BC}$的坐标,设BC与平面BDE所成角为θ,那么由sinθ=$|cos<\overrightarrow{BC},\overrightarrow{n}>|$即可求出BC与平面BDE所成角的正弦值.
解答 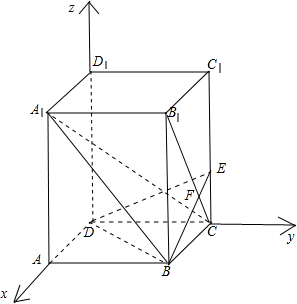 解:(1)证明:分别以边DA,DC,DD1所在直线为x,y,z轴,建立如图所示空间直角坐标系,则:
解:(1)证明:分别以边DA,DC,DD1所在直线为x,y,z轴,建立如图所示空间直角坐标系,则:
D(0,0,0),B(2,2,0),C(0,2,0),A1(2,0,4),B1(2,2,4);
E在棱CC1上,设E(0,2,z),∵BE⊥B1C,$\overrightarrow{BE}=(-2,0,z)$,$\overrightarrow{{B}_{1}C}=(-2,0,-4)$;
∴$\overrightarrow{BE}•\overrightarrow{{B}_{1}C}$=4-4z=0;
∴z=1;
∴E(0,2,1);
设平面BDE的法向量为$\overrightarrow{n}=(x,y,z)$,$\overrightarrow{DB}=(2,2,0),\overrightarrow{DE}=(0,2,1)$,则:
$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DB}=2x+2y=0}\\{\overrightarrow{n}•\overrightarrow{DE}=2y+z=0}\end{array}\right.$;
取y=1,则$\overrightarrow{n}=(-1,1,-2)$;
∴$\overrightarrow{{A}_{1}C}=(-2,2,-4)$=$2\overrightarrow{n}$;
∴$\overrightarrow{{A}_{1}C}$∥$\overrightarrow{n}$;
∴A1C⊥平面BDE;
(2)$\overrightarrow{BC}=(-2,0,0)$,设直线BC和平面BDE所成角为θ,则:
$sinθ=|cos<\overrightarrow{BC},\overrightarrow{n}>|$=$\frac{|\overrightarrow{BC}•\overrightarrow{n}|}{|\overrightarrow{BC}||\overrightarrow{n}|}=\frac{2}{2•\sqrt{6}}=\frac{\sqrt{6}}{6}$;
∴BC与平面BDE所成角的正弦值为$\frac{\sqrt{6}}{6}$.
点评 考查通过建立空间直角坐标系,利用空间向量证明线面垂直,求线面角的方法,平面法向量的概念及求法,知道直线与平面垂直时,直线方向向量与平面法向量的关系,弄清直线和平面所成角与直线方向向量和平面法向量夹角的关系,以及向量夹角夹角的坐标公式.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案| A. | (1,1) | B. | (1,-l) | C. | (-l,1) | D. | (-l,-l) |
| A. | ($\frac{π}{2}$,0) | B. | (0,1) | C. | (0,0) | D. | (-$\frac{π}{4}$,0) |
| A. | 126 | B. | 26 | C. | 13 | D. | 12 |