题目内容
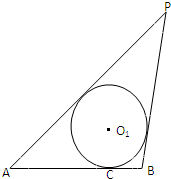
如图:已知线段AB=4,动圆O1与线段AB相切于点C,且AC-BC=2
,过点A,B分别作⊙O1的切线,两切线相交于点P,且P、O1均在AB的同侧.
(Ⅰ)建立适当坐标系,当O1位置变化时,求动点P的轨迹E方程;
(Ⅱ)过点B作直线交曲线E于点M、N,求△AMN面积的最小值.
| 2 |
(Ⅰ)建立适当坐标系,当O1位置变化时,求动点P的轨迹E方程;
(Ⅱ)过点B作直线交曲线E于点M、N,求△AMN面积的最小值.

(Ⅰ)以AB为x轴,AB的垂直平分线为y轴,建立坐标系,则|PA|-|PB|=|AC|-|BC|=2
,
∴点P在以A、B为焦点双曲线上,且2c=4,2a=2
,
∴c=2,a=
,
∴b=
=
∴P点的轨迹E为:
-
=1(x>
);
(Ⅱ)设M(x1,y1),N(x2,y2),直线:x=my+2代入双曲线
-
=1得(m2-1)y2+4my+2=0,显然m≠±1
∵M、N在双曲线一支上,∴|m|<1.
S△AMN=
×|AB|×|y1-y2|=2
=2
令t=m2+1,有1≤t<2,则S△AMN=2
=2
在[1,2)上递增
∴当t=1,即m=0时,△AMN面积取得最小值为4
.

| 2 |
∴点P在以A、B为焦点双曲线上,且2c=4,2a=2
| 2 |
∴c=2,a=
| 2 |
∴b=
| c2-a2 |
| 2 |
∴P点的轨迹E为:
| x2 |
| 2 |
| y2 |
| 2 |
| 2 |
(Ⅱ)设M(x1,y1),N(x2,y2),直线:x=my+2代入双曲线
| x2 |
| 2 |
| y2 |
| 2 |
∵M、N在双曲线一支上,∴|m|<1.
S△AMN=
| 1 |
| 2 |
|
|
令t=m2+1,有1≤t<2,则S△AMN=2
|
|
∴当t=1,即m=0时,△AMN面积取得最小值为4
| 2 |


练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
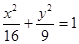 的焦点为顶点,以该椭圆的顶点为焦点的双曲线方程是 .
的焦点为顶点,以该椭圆的顶点为焦点的双曲线方程是 .