��Ŀ����
����Ŀ��ijˮ��Ʒ����������ij�����㣬�ۼ�Ϊÿ����![]() Ԫ���ɱ�Ϊÿ����
Ԫ���ɱ�Ϊÿ����![]() Ԫ��������ּ�ǵ�������������ۣ��������������ȥ��δ�۳���ȫ�����۴����꣬ƽ��ÿ������ʧ
Ԫ��������ּ�ǵ�������������ۣ��������������ȥ��δ�۳���ȫ�����۴����꣬ƽ��ÿ������ʧ![]() Ԫ�����������������������
Ԫ�����������������������![]() ��
��![]() ��
��![]() ��
��![]() ��
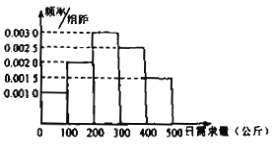
��![]() ���з��飬�õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
���з��飬�õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
��1������Ƶ�ʷֲ�ֱ��ͼ���������������������ƽ����![]() ��ͬһ���е������ø��������е�ֵ��������
��ͬһ���е������ø��������е�ֵ��������
��2���þ�����ij�칺����![]() �����������㣬���赱���������Ϊ
�����������㣬���赱���������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() Ԫ����
Ԫ����![]() ����
����![]() �ĺ�����ϵʽ�������Ƶ�ʷֲ�ֱ��ͼ��������
�ĺ�����ϵʽ�������Ƶ�ʷֲ�ֱ��ͼ��������![]() ��С��
��С��![]() Ԫ�ĸ��ʣ�
Ԫ�ĸ��ʣ�
���𰸡�(1)265;(2)0.7.
��������
�����������1��ÿ�����ε��е��������þ��ε���������˺���ͣ����ɵõ�������������������ƽ��������2��������������ۣ��������۶���ɱ��IJ����� ![]() ����
����![]() �ĺ�����ϵʽ����������
�ĺ�����ϵʽ����������![]() ��С��
��С��![]() Ԫ�����
Ԫ�����![]() ������ֱ��ͼ�����ʿɵ�����
������ֱ��ͼ�����ʿɵ�����![]() ��С��
��С��![]() Ԫ�ĸ��ʣ����ں��������ε����֮�ͣ��Ӷ��ɵý��.
Ԫ�ĸ��ʣ����ں��������ε����֮�ͣ��Ӷ��ɵý��.
���������������x��50��0.0010��100��150��0.0020��100��250��0.0030��100��350��0.0025��100��450��0.0015��100��265��
��������������������300����ʱ������Y��(20��15)��300��1500Ԫ��
��������������300����ʱ������Y��(20��15)x��(300��x)��3��8x��900Ԫ��
��Y��![]() ,
,
��Y��700����200��x��500��
����P(Y��700)��P(200��x��500)
��0.0030��100��0.0025��100��0.0015��100��0.7��

 ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�