题目内容
如图，AB和BC分别与圆O相切于点D，C，AC经过圆心O，且BC＝2OC.求证：AC＝2AD.
见解析
【解析】
证明 连接OD.
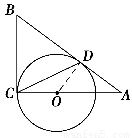
因为AB和BC分别与圆O相切于点D，C，所以∠ADO＝∠ACB＝90°.又因为∠A＝∠A，所以Rt△ADO∽Rt△ACB.
所以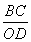
＝
.
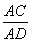又BC＝2OC＝2OD，故AC＝2AD.
练习册系列答案
黄冈冠军课课练系列答案
相关题目
黄冈冠军课课练系列答案题目内容
如图，AB和BC分别与圆O相切于点D，C，AC经过圆心O，且BC＝2OC.求证：AC＝2AD.
见解析
【解析】
证明 连接OD.
因为AB和BC分别与圆O相切于点D，C，所以∠ADO＝∠ACB＝90°.又因为∠A＝∠A，所以Rt△ADO∽Rt△ACB.
所以＝.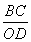
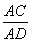又BC＝2OC＝2OD，故AC＝2AD.
黄冈冠军课课练系列答案
