题目内容
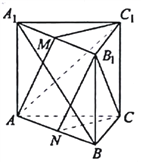
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点,求证:
的中点,求证:
(1)![]() 平面
平面![]() ;
;
(2)![]() ;
;
(3)平面![]() 平面
平面![]() .
.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】试题分析: 1)根据线面垂直的判定定理即可证明C1M⊥平面AA1B1B;
(2)根据线面垂直的性质先证明A1B⊥平面AC1M,即可证明A1B⊥AM;
(3)根据面面平行的判定定理即可证明平面AC1M∥平面B1NC.
试题解析:
(1)证法一:由直三棱柱![]() 得
得
![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]()
![]() ,
,
又∵![]() ,
,![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
又∵![]() ,
,
∴![]() 平面
平面![]() .
.
证法二:由直三棱柱![]() 得
得
平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
∵![]() ,
,![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)由(1)知,![]() 平面
平面![]()
∵![]() 平面
平面![]() ,
,
∴![]()
![]() ,
,
∵![]()
![]() ,
,![]()
![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
(3)证法一:由直三棱柱![]() 知,四边形
知,四边形![]() 是矩形,
是矩形,
∵![]() 分别是
分别是![]() 的中点,
的中点,
∴![]() ,且
,且![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
连接![]() ,则四边形
,则四边形![]() 是矩形,
是矩形,
∴![]() ,且
,且![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,且
,且![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]()
又∵![]() ,
,
∴平面![]() 平面
平面![]() .
.
证法二:由(2)知,![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]()
![]() ,
,
∵![]() ,∴
,∴![]()
![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]()
![]() ,
,
∵![]()
![]() ,
,
∴![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
点睛: 垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行,需转化为证明线线平行.
(2)证明线面垂直,需转化为证明线线垂直.
(3)证明线线垂直,需转化为证明线面垂直.

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),规定80分及以上者晋级成功,否则晋级失败(满分为100分).

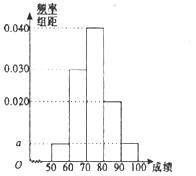
(1)求图中![]() 的值;
的值;
(2)估计该次考试的平均分![]() (同一组中的数据用该组的区间中点值代表);
(同一组中的数据用该组的区间中点值代表);
(3)根据已知条件完成下面![]() 列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
(参考公式: 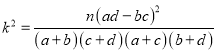 ,其中
,其中![]() )
)
| 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
【题目】某单位附近只有甲、乙两个临时停车场,它们各有![]() 个车位,为了方便市民停车,某互联网停车公司对这两个停车场,在某些固定时刻的剩余停车位进行记录,如下表:
个车位,为了方便市民停车,某互联网停车公司对这两个停车场,在某些固定时刻的剩余停车位进行记录,如下表:
时间 停车场 |
|
|
|
|
|
|
甲停车场 |
|
|
|
|
|
|
乙停车场 |
|
|
|
|
|
|
如果表中某一时刻剩余停车位数低于该停车场总车位数的![]() ,那么当车主驱车抵达单位附近时,该公司将会向车主发出停车场饱和警报.
,那么当车主驱车抵达单位附近时,该公司将会向车主发出停车场饱和警报.
(1)假设某车主在以上六个时刻抵达单位附近的可能性相同,求他收到甲停车场饱和警报的概率;
(2)从这六个时刻中任选一个时刻,求甲停车场比乙停车场剩余车位数少的概率;
(3)当乙停车场发出饱和警报时,求甲停车场也发出饱和警报的概率.