Question

【题目】如图空间四边形ABCD，E、F、G、H分别为AB、AD、CB、CD的中点且AC=BD，AC⊥BD，试判断四边形EFGH的形状，并证明．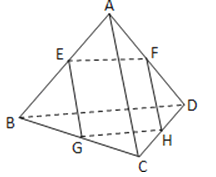

Answer 1

【答案】证明：四边形EFGH为正方形．下面给出证明：
∵E、F、G、H分别为AB、AD、CB、CD的中点，
∴，，
∴．
∴四边形EFGH是平行四边形．
同理可证：．
∵AC=BD，BD⊥AC，
∴EF=EG，EF⊥EG．
∴平行四边形EFGH是正方形．
【解析】由于E、F、G、H分别为AB、AD、CB、CD的中点，利用三角形的中位线定理可证明：四边形EFGH是平行四边形．
由AC=BD，BD⊥AC，可证明：EF=EG，EF⊥EG．因此四边形EFGH是正方形．
【考点精析】利用平行公理对题目进行判断即可得到答案，需要熟知平行于同一条直线的两条直线互相平行．