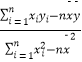题目内容
【题目】已知集合A={x|a﹣1＜x＜2a+1}，B={x|0＜x＜1}
（1）若a=
， 求A∩B．
（2）若A∩B=，求实数a的取值范围．
【答案】解：（1）当a=
时，A={x|-＜x＜2}，B={x|0＜x＜1}
∴A∩B={x|0＜x＜1}
（2）若A∩B=
当A=时，有a﹣1≥2a+1
∴a≤﹣2
当A≠时，有
∴﹣2＜a≤-或a≥2
综上可得，a≤或a≥2
【解析】（1）当a=时，A={x|-＜x＜2}，可求A∩B
（2）若A∩B=，则A=时，A≠时，有 ， 解不等式可求a的范围
【考点精析】本题主要考查了集合的交集运算的相关知识点，需要掌握交集的性质：（1）A∩B
A，A∩BB，A∩A=A，A∩
=,A∩B=B∩A;（2）若A∩B=A，则AB，反之也成立才能正确解答此题．
练习册系列答案
相关题目
