题目内容
15.试求与圆C1:(x-1)2+y2=1相外切,且与直线x+$\sqrt{3}$y=0相切于点Q(3,-$\sqrt{3}$)的圆的方程.分析 设圆心为(x,$\sqrt{3}$x-4$\sqrt{3}$),半径为R,利用两圆外切及直线与圆相切建立方程组,求出参数,得到所求的圆的方程.
解答 解:依题意,且由切线性质得:圆心所在的直线与直线x+$\sqrt{3}$y=0垂直.
设圆心所在的直线方程是y+$\sqrt{3}$=$\sqrt{3}$(x-3),即y=$\sqrt{3}$x-4$\sqrt{3}$
设圆心为(x,$\sqrt{3}$x-4$\sqrt{3}$),半径为R,则
①(x-3)2+($\sqrt{3}$x-4$\sqrt{3}$+$\sqrt{3}$)2=R2,
②(x-1)2+($\sqrt{3}$x-4$\sqrt{3}$)2=(R+1)2,
①-②得到x=6-R,
再把x=6-R代入①得到R2-8R+12=0,
解得R1=6,R2=2,
所以解得x1=0,x2=4,
所以当R=6时圆心坐标为(0,-4$\sqrt{3}$),当R=2时,圆心坐标为(4,0),
所以圆的方程为x2+(y+4$\sqrt{3}$)2=36或(x-4)2+y2=4.
点评 一般情况下,如果已知圆心(或易于求出)或圆心到某一直线的距离(或易于求出),可用圆的标准方程来求解,用待定系数法求出圆心坐标和半径.

练习册系列答案
相关题目
6.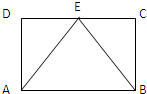 如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机抽取一个点Q,则点Q取自△ABE内部的概率等于( )
如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机抽取一个点Q,则点Q取自△ABE内部的概率等于( )
 如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机抽取一个点Q,则点Q取自△ABE内部的概率等于( )
如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机抽取一个点Q,则点Q取自△ABE内部的概率等于( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
3.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 57600 | B. | 576000 | C. | 41600 | D. | 1600(22+$\sqrt{17}$) |
4.圆x2+y2=9与圆(x-1)2+(y+1)2=16的位置关系是( )
| A. | 相交 | B. | 内切 | C. | 外切 | D. | 相离 |
 已知直二面角α-l-β,点A∈α,AC⊥l,C为垂足,点B∈α,BD⊥l,D为垂足,若AB=2,AC=BD=1,求D到平面ABC的距离.
已知直二面角α-l-β,点A∈α,AC⊥l,C为垂足,点B∈α,BD⊥l,D为垂足,若AB=2,AC=BD=1,求D到平面ABC的距离.