题目内容
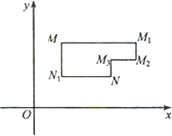
在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径成为M到N的一条“L路径”.如图所示的路径MM1M2M3N与路径MN1N都是M到N的“L路径”.某地有三个新建的居民区,分别位于平面xOy内三点A(3,20),B(-10,0),C(14,0)处.现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心.
(Ⅰ)写出点P到居民区A的“L路径”长度最小值的表达式(不要求证明);
(Ⅱ)若以原点O为圆心,半径为1的圆的内部是保护区,“L路径”不能进入保护区,请确定点P的位置,使其到三个居民区的“L路径”长度值和最小.
答案:
解析:
解析:
答案:(Ⅰ)d=|x-3|+|y-20|,y≥0,x∈R.
(Ⅱ)当点P(x,y)满足P(3,1)时,其到三个居民区的“L路径”长度值和最小为45
解析:![]()
(Ⅰ)![]() ,
,
![]() ,其中
,其中![]()
(Ⅱ)本问考查分析解决应用问题的能力,以及绝对值的基本知识.
点P到A,B,C三点的“L路径”长度之和的最小值d=水平距离之和的最小值h+垂直距离之和的最小值v.且h和v互不影响.显然当y=1时,v=20+1=21;![]() ,水平距离之和h=x-(-10)+14-x+|x-3|≥24,且当x=3时,h=24.因此,当P(3,1)时,d=21+24=45.
,水平距离之和h=x-(-10)+14-x+|x-3|≥24,且当x=3时,h=24.因此,当P(3,1)时,d=21+24=45.
所以,当点P(x,y)满足P(3,1)时,点P到A,B,C三点的“L路径”长度之和d的最小值为45.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是