题目内容
已知函数y=-x2+2|x|+2
(1)作出该函数的图象;
(2)由图象指出该函数的单调区间;
(3)由图象指出当x取何值时,函数有最值,并求出最值.
(1)作出该函数的图象;
(2)由图象指出该函数的单调区间;
(3)由图象指出当x取何值时,函数有最值,并求出最值.
分析:(1)由题意得y=
,正确画出图象.
(2)结合函数的图象,写出函数的单调区间.
(3)由图象可得当x=±1时,函数有最大值为3.
|
(2)结合函数的图象,写出函数的单调区间.
(3)由图象可得当x=±1时,函数有最大值为3.
解答:解:(1)由题意得y=
,正确画出图象得(5分);如图所示:
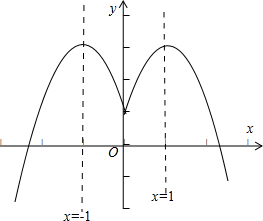
(2)函数的单调递增区间为(-∞,-1]和[0,1],(9分) 单调递减区间为(-1,0)和(1,+∞).(13分)
(3)由图象可得当x=±1时,函数有最大值为3.(15分)
|
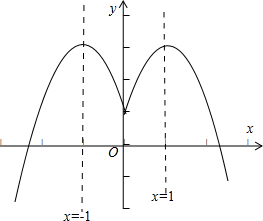
(2)函数的单调递增区间为(-∞,-1]和[0,1],(9分) 单调递减区间为(-1,0)和(1,+∞).(13分)
(3)由图象可得当x=±1时,函数有最大值为3.(15分)
点评:本题主要考查函数的图象和性质应用,体现了分类讨论、数形结合的数学思想,属于中档题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目