题目内容
已知函数y=x2-x-4的定义域为[m,n],值域为[-
,-4],则m+n的取值范围为( )
| 17 |
| 4 |
分析:将二次函数进行配方,利用值域确定m,n的取值范围.
解答:解:∵y=f(x)=x2-x-4=(x-
)2-
.
∴由y=f(x)=x2-x-4=-4得x2-x=0,解得x=0或x=1.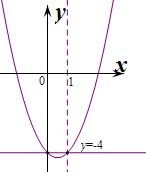
当x=
时,函数取得最小值-
.
∵值域为[-
,-4],
∴对称轴
∈[m,n],
∴若m=0,则
≤n≤1,此时
≤m+n≤1.
若n=1,则0≤m≤
,此时1≤m+n≤
,
综上:
≤m+n≤
,即m+n的取值范围为[
,
].
故选B.
| 1 |
| 2 |
| 17 |
| 4 |
∴由y=f(x)=x2-x-4=-4得x2-x=0,解得x=0或x=1.

当x=
| 1 |
| 2 |
| 17 |
| 4 |
∵值域为[-
| 17 |
| 4 |
∴对称轴
| 1 |
| 2 |
∴若m=0,则
| 1 |
| 2 |
| 1 |
| 2 |
若n=1,则0≤m≤
| 1 |
| 2 |
| 3 |
| 2 |
综上:
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
故选B.
点评:本题主要考查二次函数的图象和性质,利用值域确定定义域的取值范围是解决本题的关键,利用数形结合是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目