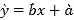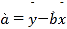题目内容
【题目】已知函数![]() .
.
(Ⅰ)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(Ⅱ)设函数![]() ,在(Ⅰ)的条件下,试判断
,在(Ⅰ)的条件下,试判断![]() 在
在![]() 上是否存在极值.若存在,判断极值的正负;若不存在,请说明理由.
上是否存在极值.若存在,判断极值的正负;若不存在,请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)当
;(Ⅱ)当![]() 时,
时, ![]() 在
在![]() 上不存在极值;当
上不存在极值;当![]() 时,
时, ![]() 在
在![]() 上存在极值,且极值均为正.
上存在极值,且极值均为正.
【解析】试题分析:(1)不等式恒成立问题,一般先利用变量分离转化为对应函数最值问题: ![]() 的最大值,利用导数研究函数
的最大值,利用导数研究函数![]() 最值,易得
最值,易得![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,因此
,因此![]() ,(2)即研究
,(2)即研究![]() 导函数的零点情况,先求导数,确定研究对象为
导函数的零点情况,先求导数,确定研究对象为![]() ,再求目标函数导数,确定单调性:先增后减,两个端点值都小于零,讨论最大值是否大于零,最后结合零点存在定理确定极值点个数.
,再求目标函数导数,确定单调性:先增后减,两个端点值都小于零,讨论最大值是否大于零,最后结合零点存在定理确定极值点个数.
试题解析:解:(Ⅰ)由![]() ,得
,得![]() .
.
即![]() 在
在![]() 上恒成立.
上恒成立.
设函数![]() ,
, ![]() .
.
则![]() .
.
∵![]() ,∴
,∴![]() .
.
∴当![]() 时,
时, ![]() .
.
∴![]() 在
在![]() 上单调递减.
上单调递减.
∴当![]() 时,
时, ![]() .
.
∴![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .
.
(Ⅱ)![]() ,
, ![]() .
.
∴![]() .
.
设![]() ,则
,则![]() .
.
由![]() ,得
,得![]() .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
且![]() ,
, ![]() ,
, ![]() .
.
据(Ⅰ),可知![]() .
.
(ⅰ)当![]() ,即
,即![]() 时,
时, ![]() 即
即![]() .
.
∴![]() 在
在![]() 上单调递减.
上单调递减.
∴当![]() 时,
时, ![]() 在
在![]() 上不存在极值.
上不存在极值.
(ⅱ)当![]() ,即
,即![]() 时,
时,
则必定![]() ,使得
,使得![]() ,且
,且![]() .
.
当![]() 变化时,
变化时, ![]() ,
, ![]() ,
, ![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
| - | 0 | + | 0 | - |
| - | 0 | + | 0 | - |
| ↘ | 极小值 | ↗ | 极大值 | ↘ |
∴当![]() 时,
时, ![]() 在
在![]() 上的极值为
上的极值为![]() ,且
,且![]() .
.
∵![]() .
.
设![]() ,其中
,其中![]() ,
, ![]() .
.
∵![]() ,∴
,∴![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
∵![]() ,∴
,∴![]() .
.
∴当![]() 时,
时, ![]() 在
在![]() 上的极值
上的极值![]() .
.
综上所述:当![]() 时,
时, ![]() 在
在![]() 上不存在极值;当
上不存在极值;当![]() 时,
时, ![]() 在
在![]() 上存在极值,且极值均为正.
上存在极值,且极值均为正.
注:也可由![]() ,得
,得![]() .令
.令![]() 后再研究
后再研究![]() 在
在![]() 上的极值问题.
上的极值问题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目