题目内容
(2011•惠州模拟)设平面区域D是由双曲线y2-
=1的两条渐近线和抛物线y2=-8x的准线所围成的三角形(含边界与内部).若点(x,y)∈D,则目标函数z=x+y的最大值为
| x2 | 4 |
3
3
.分析:根据双曲线的渐近线公式和抛物线准线的公式,求出三条直线方程,从而得到可行域是图中△ABO及其内部,然后利用直线平移法,即可求得目标函数z=x+y的最大值.
解答:解:∵双曲线
-
=1的渐近线方程为y=±
x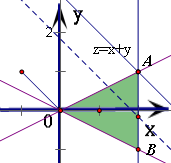
∴双曲线y2-
=1的两条渐近线为:y=±
x,
∵抛物线y2=-2px的准线为x=
,
∴抛物线y2=-8x的准线为x=2,
因此作出三条直线,得可行域是△ABO及其内部(如图)
将直线l:z=x+y,即y=-x+z进行平移,可得
当直线y=-x+z过点A(2,1)时,目标函数z=x+y有最大值
∴zmax=F(2,1)=2+1=3.
故答案为:3
| y2 |
| a2 |
| x2 |
| b2 |
| a |
| b |

∴双曲线y2-
| x2 |
| 4 |
| 1 |
| 2 |
∵抛物线y2=-2px的准线为x=
| p |
| 2 |
∴抛物线y2=-8x的准线为x=2,
因此作出三条直线,得可行域是△ABO及其内部(如图)
将直线l:z=x+y,即y=-x+z进行平移,可得
当直线y=-x+z过点A(2,1)时,目标函数z=x+y有最大值
∴zmax=F(2,1)=2+1=3.
故答案为:3
点评:本题以简单的线性规划为载体,求目标函数的最大值,着重考查了双曲线、抛物线的标准方程和基本概念和简单的线性规划等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011•惠州模拟)从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图由图中数据可知身高在[120,130]内的学生人数为( )
(2011•惠州模拟)从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图由图中数据可知身高在[120,130]内的学生人数为( ) (2011•惠州模拟)如图,在正方体AC1中,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( )
(2011•惠州模拟)如图,在正方体AC1中,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( )