题目内容
函数y = 1n|x-1|的图像与函数y="-2" cos  x(-2≤x≤4)的图像所有交点的横坐标之和等于
x(-2≤x≤4)的图像所有交点的横坐标之和等于
| A.8 | B.6 | C.4 | D.2 |
B
解析试题分析:在同一平面直角坐标系中,画出函数y = 1n|x-1|的图像与函数y="-2" cos  x(-2≤x≤4)的图像,易知函数y = 1n|x-1|的图像与函数y="-2" cos
x(-2≤x≤4)的图像,易知函数y = 1n|x-1|的图像与函数y="-2" cos  x(-2≤x≤4)的图像都关于直线x=1对称,且在直线x=1的左右两侧各有3个交点,3个交点都分别关于直线x=1对称,所以所有交点的横坐标之和等于6.
x(-2≤x≤4)的图像都关于直线x=1对称,且在直线x=1的左右两侧各有3个交点,3个交点都分别关于直线x=1对称,所以所有交点的横坐标之和等于6.
考点:对数函数的图像;三角函数的图像;图像的变换;函数的性质;中点坐标公式。
点评:此题主要考查数形结合的数学思想。做此题的关键是正确、快速的画出函数y = 1n|x-1|与函数y="-2" cos  x(-2≤x≤4)的图像。属于中档题。
x(-2≤x≤4)的图像。属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数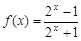 ,则不等式
,则不等式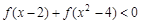 的解集为( )
的解集为( )
A.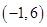 | B.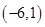 | C.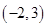 | D.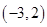 |
若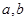 是任意实数,且
是任意实数,且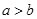 ,则( )
,则( )
A.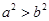 | B. | C.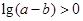 | D.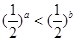 |
对函数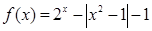 的零点个数判断正确的是 )
的零点个数判断正确的是 )
| A.1个 | B.2个 | C.3个 | D.0个 |
下列函数在其定义域内既是奇函数又是增函数的是
A.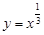 | B.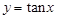 | C.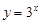 | D.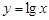 |
下列函数中,既是偶函数又在 单调递增的函数是( )
单调递增的函数是( )
A. | B. | C. | D. |
已知 且
且 ,则
,则
| A.有最大值2 | B.有最大值4 | C.有最小值3 | D.等于4 |
已知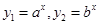 是指数函数,
是指数函数,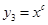 ,
, 是幂函数,它们的图象如右图所示,则
是幂函数,它们的图象如右图所示,则 的大小关系为
的大小关系为 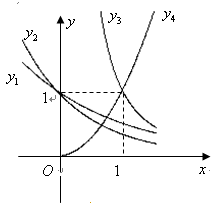
A. | B.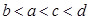 |
C.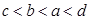 | D.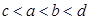 |
函数 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A. | B. | C. | D.  |