题目内容
下列函数在其定义域内既是奇函数又是增函数的是
A.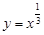 | B.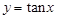 | C.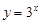 | D.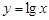 |
A
解析试题分析:对于A.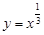 ,由于定义域为R,同时f(x)=-f(-x),因此是奇函数,同时,随着x的增大而增大,因此是符合题意的。
,由于定义域为R,同时f(x)=-f(-x),因此是奇函数,同时,随着x的增大而增大,因此是符合题意的。
对于B.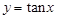 由于函数满足奇函数的性质,但是每一个周期内是递增的,不是整个定义域递增,错误。
由于函数满足奇函数的性质,但是每一个周期内是递增的,不是整个定义域递增,错误。
对于C.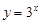 由于指数函数底数大于1,因此是增函数,但是不满足f(-x)=f(x),与f(x)=-f(-x),因此是非奇非偶函数。
由于指数函数底数大于1,因此是增函数,但是不满足f(-x)=f(x),与f(x)=-f(-x),因此是非奇非偶函数。
对于D.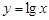 由于对数函数x>0,因此不满足定义域关于原点对称 ,因此不具有奇偶性舍去,故选A.
由于对数函数x>0,因此不满足定义域关于原点对称 ,因此不具有奇偶性舍去,故选A.
考点:本试题考查了函数的性质。
点评:解决该试题的关键是理解函数的奇偶性和单调性的判定原则,结合其性质和常见的基本初等函数的性质得到结论,属于基础题。

练习册系列答案
相关题目
下列函数中,既是奇函数又是增函数的是
A.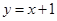 | B. | C.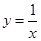 | D.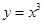 |
设函数 的定义域为实数集R,
的定义域为实数集R, ,且当
,且当 时,
时, ,则有( )
,则有( )
A.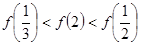 | B. |
C. | D. |
函数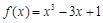 在闭区间 [-3,0] 上的最大值、最小值分别是( )
在闭区间 [-3,0] 上的最大值、最小值分别是( )
| A.1,? 1 | B.1,? 17 | C.3,? 17 | D.9,? 197 |
函数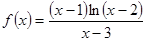 的零点有
的零点有
A. 个 个 | B. 个 个 | C.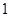 个 个 | D. 个 个 |
函数y = 1n|x-1|的图像与函数y="-2" cos  x(-2≤x≤4)的图像所有交点的横坐标之和等于
x(-2≤x≤4)的图像所有交点的横坐标之和等于
| A.8 | B.6 | C.4 | D.2 |
已知 是定义在
是定义在 上的奇函数,且当x<0时不等式
上的奇函数,且当x<0时不等式 成立,若
成立,若 ,
, 
 ,则
,则 大小关系是
大小关系是
A. | B.c > b > a | C. | D.c > a >b |
对任意的 ,则( )
,则( )
A. | B.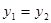 |
C. | D. 的大小不能确定 的大小不能确定 |
函数 ,则f(x)-g(x)是
,则f(x)-g(x)是
| A.奇函数 | B.偶函数 |
| C.既不是奇函数又不是偶函数 | D.既是奇函数又是偶函数 |