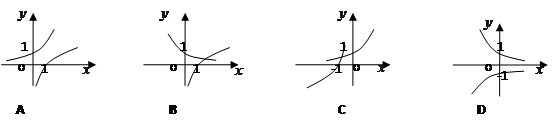题目内容
对函数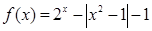 的零点个数判断正确的是 )
的零点个数判断正确的是 )
| A.1个 | B.2个 | C.3个 | D.0个 |
C
解析试题分析:由题意,可将函数f(x)=2x-|x2-1|-1的零点的个数问题转化为两个函数y=2x-1与y=|x2-1|的交点问题,作出两个函数的图象,由图象选出正确选项
由题意,函数f(x)=2x-|x2-1|-1的零点的个数即两个函数y=2x-1与y=|x2-1|的交点的个数,两个函数的图象如图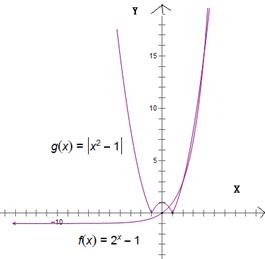
由图知,两个函数有三个交点
故函数f(x)=2x-|x2-1|-1的零点的个数是3
故选C
考点:函数零点
点评:确定函数零点的方法可以图形法,也可以利用方程的解,也可以图像与图像的交点来判定,基础题。

练习册系列答案
相关题目
设函数 为定义在R上的奇函数,当
为定义在R上的奇函数,当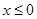 时,
时, (
( 为常数),则
为常数),则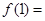 ( )
( )
| A.3 | B.1 | C.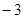 | D. |
若函数 在区间
在区间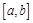 上为减函数,则
上为减函数,则 在
在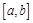 上( ).
上( ).
| A.至少有一个零点 | B.只有一个零点 |
| C.没有零点 | D.至多有一个零点 |
函数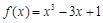 在闭区间 [-3,0] 上的最大值、最小值分别是( )
在闭区间 [-3,0] 上的最大值、最小值分别是( )
| A.1,? 1 | B.1,? 17 | C.3,? 17 | D.9,? 197 |
函数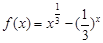 的零点个数为
的零点个数为
| A.0 | B.1 |
| C.2 | D.3 |
函数y = 1n|x-1|的图像与函数y="-2" cos  x(-2≤x≤4)的图像所有交点的横坐标之和等于
x(-2≤x≤4)的图像所有交点的横坐标之和等于
| A.8 | B.6 | C.4 | D.2 |
已知-2<x<0,则 的最小值为( )
的最小值为( )
| A.2 | B.3 | C. | D.-2 |
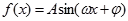 (
(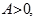
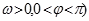 的部分图像如图所示.若△EFG为等腰直角三角形,且
的部分图像如图所示.若△EFG为等腰直角三角形,且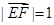 ,则
,则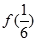 的值为 ( )
的值为 ( )

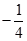
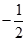
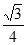
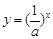 与
与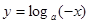 (其中
(其中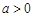 且
且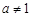 )的图象只可能是( )
)的图象只可能是( )