题目内容
7.已知f(x)=x|x-a|-2,当x∈(0,2]时恒有f(x)<0,则实数a的取值范围是1<a<3.分析 整理不等式得x-$\frac{2}{x}$<a<x+$\frac{2}{x}$恒成立,构造函数令h(x)=x-$\frac{2}{x}$,g(x)=x+$\frac{2}{x}$,x∈(0,2],把恒成立问题转换为最值问题,利用导数判断单调性,求出函数最值,得出a的范围.
解答 解:∵f(x)<0,
∴x|x-a|<2,
∴x-$\frac{2}{x}$<a<x+$\frac{2}{x}$恒成立,
令h(x)=x-$\frac{2}{x}$,g(x)=x+$\frac{2}{x}$,x∈(0,2],
∵h'(x)=1+$\frac{4}{{x}^{2}}$>0,h(x)递增,
∴h(x)≥h(2)=1,
g'(x)=1-$\frac{4}{{x}^{2}}$<0,g(x)递减,
g(x)≤g(2)=3,
∴a的取值范围是1<a<3.
点评 考查了绝对值不等,恒成立问题转换为最值问题,难点是构造函数,求函数的最值.

练习册系列答案
相关题目
17.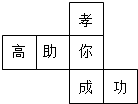 水平放置的正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示,如图是正方体的表面展开图,若图中“成”表示正方体的前面,“功”表示正方体的右面,“你”表示正方体的下面,则“孝”“高”“助”分别表示正方体的( )
水平放置的正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示,如图是正方体的表面展开图,若图中“成”表示正方体的前面,“功”表示正方体的右面,“你”表示正方体的下面,则“孝”“高”“助”分别表示正方体的( )
 水平放置的正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示,如图是正方体的表面展开图,若图中“成”表示正方体的前面,“功”表示正方体的右面,“你”表示正方体的下面,则“孝”“高”“助”分别表示正方体的( )
水平放置的正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示,如图是正方体的表面展开图,若图中“成”表示正方体的前面,“功”表示正方体的右面,“你”表示正方体的下面,则“孝”“高”“助”分别表示正方体的( )| A. | 左面,后面,上面 | B. | 后面,上面,左面 | C. | 上面,左面,后面 | D. | 后面,左面,上面 |
18.函数y=x2-2x+3,x∈[-1,3]的最大值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
15.若一条直线与两条平行直线都相交,则这三条直线确定的平面的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 1或3 |
12.正方体的八个顶点可以确定的平面个数为( )
| A. | 6 | B. | 8 | C. | 14 | D. | 20 |
19.已知集合P={x|1≤x≤3},则实数2与集合P的关系是( )
| A. | 2∈P | B. | 2∉P | C. | 2⊆P | D. | 2?P |
16.函数y=cosxsin2x的最小值为( )
| A. | -1 | B. | -$\frac{4\sqrt{3}}{9}$ | C. | -2 | D. | -$\frac{2\sqrt{3}}{9}$ |