题目内容
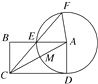
【题目】如图,在矩形ABCD中,以A为圆心,AD为半径的圆交AC,AB于M,E.CE的延长线交⊙A于F,CM=2,AB=4.
(1)求⊙A的半径;
(2)求CE的长和△AFC的面积
【答案】(1)3(2) ![]()
【解析】试题分析:(1)根据勾股定理得关于半径关系式,解得半径;(2)由直角三角形可得CE的长,由切割线定理可得CF,根据解三角形可得三角形面积
试题解析:解:(1)∵四边形ABCD为矩形,AB=4,∴CD=4.
在Rt△ACD中,AC2=CD2+AD2,
∴(2+AD)2=42+AD2.
解得:AD=3,即⊙A的半径为3.
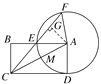 (2)过点A作AG⊥EF于点G,
(2)过点A作AG⊥EF于点G,
∵BC=3,
BE=AB-AE=4-3=1,
∴CE=![]()
=![]() =
=![]() .
.
∵∠ADC=90°,
∴CD为⊙A的切线,
∴CE·CF=CD2,
∴CF=![]() =
=![]() =
=![]()
![]() .
.
又∠B=∠AGE=90°,∠BEC=∠GEA,
∴△BCE∽△GAE,
∴![]() =
=![]() 即
即![]() =
=![]() .∴AG=
.∴AG=![]()
![]() ,
,
∴S△AFC=![]() CF·AG=
CF·AG=![]() ×
×![]()
![]() ×
×![]()
![]() =
=![]() .
.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关,通过随机抽查110名学生,得到如下![]() 的列联表:
的列联表:
喜欢该项运动 | 不喜欢该项运动 | 总计 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由公式 ,算得
,算得![]()
附表:
| 0.025 | 0.01 | 0.005 |
| 5.024 | 6.635 | 7.879 |
参照附表,以下结论正确的是( )
A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错语的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
C. 有99%以上的把握认为“爱好该项运动与性别无关”
D. 有99%以上的把握认为“爱好该项运动与性别有关”