��Ŀ����
����Ŀ����֪����f��x���Ķ�������D�������ڳ���m��M��ʹ��m��f��x����M������x��D��������ƺ���f��x����D�ϵ��н纯��������m��Ϊ����f��x�����½磬M��Ϊ����f��x�����Ͻ磻�ر�أ�����=����������m��Ϊ����f��x������ȷ�磬M��Ϊ����f��x������ȷ�磮 �����ж� ![]() �Ƿ����н纯����˵�����ɣ�
�Ƿ����н纯����˵�����ɣ�
����������f��x��=1+a2x+4x��x�ʣ����ޣ�0�������ԩ�3Ϊ�½硢3Ϊ�Ͻ���н纯������ʵ��a��ȡֵ��Χ��
���������� ![]() ��T��a����f��x������ȷ�磬��T��a����ȡֵ��Χ��
��T��a����f��x������ȷ�磬��T��a����ȡֵ��Χ��
���𰸡��⣺����f��x��= ![]() ��
�� ![]() =
= ![]() �� ��x��0����
�� ��x��0���� ![]() +
+ ![]() ��1��
��1��
��0��f��x����1������f��x�����н纯����
��t=3x �� ��t��0��
��y=t2��3t�ݩ�1��g��x����[��1��+�ޣ���
��g��x�������н纯����
���ߺ���f��x��=1+a2x+4x �� ��x�ʣ����ޣ�0�������ԩ�3Ϊ�½磬3Ϊ�Ͻ���н纯����
�ੁ3��1+a2x+4x��3�ڣ����ޣ�0���Ϻ������
����2x�� ![]() ��a��
��a�� ![]() ��2x�ڣ����ޣ�0���Ϻ������
��2x�ڣ����ޣ�0���Ϻ������
��t=2x �� g��t��=��t�� ![]() ��h��t��=��t+
��h��t��=��t+ ![]() ��
��
��x��0����0��t��1��
��t1 �� t2�ʣ�0��1������t1��t2 ��
��g��t1����g��t2��= ![]() ��0��
��0��
��g��t���ڣ�0��1��������
��g��t����g��1��=��5����a�ݩ�5��h��t1����h��t2����0��
��h��t���ڣ�0��1�����Ǽ�������
��h��t����h��1��=1��
��a��1��
���ϣ�ʵ��a�ķ�Χ��[��5��1]��
������y= ![]() ���ã�a2x=
���ã�a2x= ![]() ��
��
��x��[0��1]��a��0��
��a��a2x��2a��
��a�� ![]() ��2a��
��2a��
�� ![]() ��y��
��y�� ![]() ��
��
��T��a��= ![]() =��1+
=��1+ ![]() ��
��
��a��0��
��T��a���ķ�Χ�ǣ���1��1��
���������������н纯���Ķ���ֱ����f��x����g��x���ķ�Χ���Ӷ��ж��Ƿ��н缴�ɣ���������ת��Ϊ��2x�� ![]() ��a��
��a�� ![]() ��2x�ڣ����ޣ�0���Ϻ��������t=2x �� g��t��=��t��
��2x�ڣ����ޣ�0���Ϻ��������t=2x �� g��t��=��t�� ![]() ��h��t��=��t+
��h��t��=��t+ ![]() �����ݺ����ĵ��������t�ķ�Χ���ɣ��������a��
�����ݺ����ĵ��������t�ķ�Χ���ɣ��������a�� ![]() ��2a������
��2a������ ![]() ��y��
��y�� ![]() ���õ�T��a��=
���õ�T��a��= ![]() ���Ӷ����T��a���ķ�Χ���ɣ�
���Ӷ����T��a���ķ�Χ���ɣ�
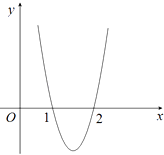
�����㾫�������ú�������ֵ���伸���������Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪���ö��κ��������ʣ��䷽�������������С��ֵ������ͼ�����������С��ֵ�����ú��������Ե��жϺ��������С��ֵ��

����Ŀ���������ij�豸��ʹ������x���꣩����֧����ά����y����Ԫ�������µ�ͳ�����ϣ�
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
��1������ɢ��ͼ���ж��Ƿ�������أ�
��2�����������أ������Իع鷽�̣�
��3������ʹ������Ϊ10��ʱ��ά�����Ƕ��٣�