题目内容
已知数列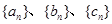 满足
满足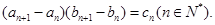
(1)设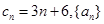 是公差为
是公差为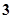 的等差数列.当
的等差数列.当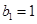 时,求
时,求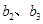 的值;
的值;
(2)设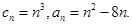 求正整数
求正整数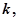 使得一切
使得一切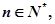 均有
均有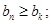
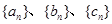 满足
满足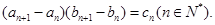
(1)设
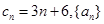 是公差为
是公差为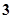 的等差数列.当
的等差数列.当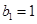 时,求
时,求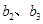 的值;
的值;(2)设
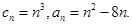 求正整数
求正整数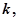 使得一切
使得一切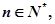 均有
均有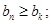
(1) (2)
(2)
 (2)
(2)
试题分析::(1)
 ,
,
(2)由
 ,
, 由
 ,即
,即 ;
;由
 ,即
,即
 .
. 点评:本题考查数列递推式,考查数列的求和,考查恒成立问题,确定数列通项是解题的关键

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
题目内容
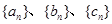 满足
满足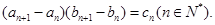
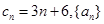 是公差为
是公差为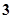 的等差数列.当
的等差数列.当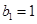 时,求
时,求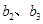 的值;
的值;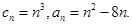 求正整数
求正整数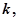 使得一切
使得一切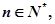 均有
均有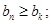
 (2)
(2)
 ,
,
 ,
,  ,即
,即 ;
; ,即
,即
 .
. 
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案