题目内容
已知函数 ,数列
,数列 满足
满足 。
。
(1)求 ;
;
(2)猜想数列 的通项公式,并用数学归纳法予以证明。
的通项公式,并用数学归纳法予以证明。
 ,数列
,数列 满足
满足 。
。(1)求
 ;
;(2)猜想数列
 的通项公式,并用数学归纳法予以证明。
的通项公式,并用数学归纳法予以证明。(1)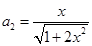 ,
,
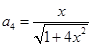
(2)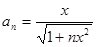
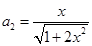 ,
,
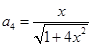
(2)
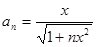
试题分析:解:(1)由
 得:
得: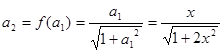 ,
,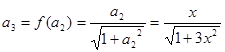
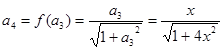 .4分
.4分(2)猜想数列
 的通项公式
的通项公式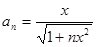 。
。证明:(1)当
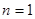 时,结论显然成立;
时,结论显然成立;(2)假设当
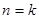 时,结论成立,即
时,结论成立,即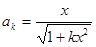 。
。则当
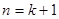 时,
时,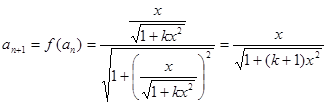 。
。显然,当
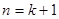 时,结论成立。
时,结论成立。由(1)、(2)可得,数列
 的通项公式
的通项公式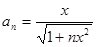 。 .13分
。 .13分点评:主要是考查了数列递推关系来求解项,并归纳猜想数列的通项公式,以及数学归纳法的证明。属于中档题。

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
 中,
中, 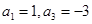
 项和
项和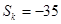 ,求
,求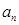 }中,
}中,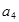 =14,前10项和
=14,前10项和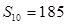 . (1)求
. (1)求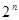 项按原来的顺序排成一个新数列{
项按原来的顺序排成一个新数列{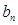 },令
},令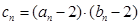 ,求数列{
,求数列{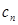 }的前
}的前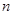 项和
项和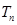 .
.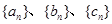 满足
满足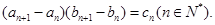
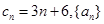 是公差为
是公差为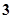 的等差数列.当
的等差数列.当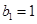 时,求
时,求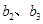 的值;
的值;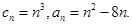 求正整数
求正整数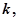 使得一切
使得一切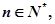 均有
均有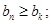
 中,
中, ,公差
,公差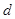 为整数,若
为整数,若 ,
, .
. 项和
项和 的最大值;
的最大值; 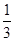 ,则D(3ξ-1)=( )
,则D(3ξ-1)=( )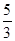 C、
C、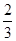 D、5
D、5 }满足
}满足 ,其中
,其中 为实常数,则数列{
为实常数,则数列{ 的通项公式是
的通项公式是 ,若前n项的和为11,则n=______
,若前n项的和为11,则n=______ 的前
的前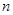 项之和
项之和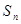 满足
满足 ,那么
,那么  .
.