题目内容
【题目】袋中有外形、质量完全相同的红球、黑球、黄球、绿球共12个．从中任取一球，得到红球的概率是 
，得到黑球或黄球的概率是 
，得到黄球或绿球的概率也是 ．
（1）试分别求得到黑球、黄球、绿球的概率；
（2）从中任取一球，求得到的不是“红球或绿球”的概率．
【答案】
（1）解：从12个球中任取一个，
记事件A=“得到红球”，事件B=“得到黑球”，事件C=“得到黄球”，事件D=“得到绿球”，
则事件A、B、C、D两两互斥，
由题意有：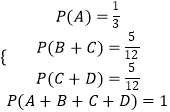 
，
即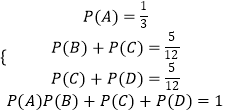 
，
解得 
， 
， 
， 
，
故得到黑球、黄球、绿球的概率分别为 
、 
、
（2）解：事件“得到红球或绿球”可表示为事件“A+D”，
由（1）及互斥事件概率加法公式得：
，
故得到的不是“红球或绿球”的概率：
【解析】（1）从12个球中任取一个，记事件A=“得到红球”，事件B=“得到黑球”，事件C=“得到黄球”，事件D=“得到绿球”，则事件A、B、C、D两两互斥，由此能求出得到黑球、黄球、绿球的概率．（2）事件“得到红球或绿球”可表示为事件“A+D”，由互斥事件概率加法公式和对立事件概率计算公式能求出得到的不是“红球或绿球”的概率．
阅读快车系列答案
【题目】为研究冬季昼夜温差大小对某反季节大豆新品种发芽率的影响，某农科所记录了5组昼夜温差与100颗种子发芽数，得到如表资料：
组号 | 1 | 2 | 3 | 4 | 5 |
温差x（°C） | 10 | 11 | 13 | 12 | 8 |
发芽数y（颗） | 23 | 25 | 30 | 26 | 16 |
该所确定的研究方案是：先从这五组数据中选取2组，用剩下的3组数据求出线性回归方程，再对被选取的2组数据进行检验．
（1）若选取的是第1组与第5组的两组数据，请根据第2组至第4组的数据，求出y关于x的线性回归方程 
；
（2）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问（1）中所得的线性回归方程是否可靠？
（参考公式： 
= 
= 
， 
）
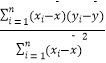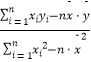