题目内容
【题目】记等比数列{an}前n项和为Sn ， 已知a1+a3=30，3S1 ， 2S2 ， S3成等差数列．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足b1=3，bn+1﹣3bn=3an ， 求数列{bn}的前n项和Bn；
（3）删除数列{an}中的第3项，第6项，第9项，…，第3n项，余下的项按原来的顺序组成一个新数列，记为{cn}，{cn}的前n项和为Tn ， 若对任意n∈N* ， 都有 
＞a，试求实数a的最大值．
【答案】
（1）解：设等比数列{an}的公比为q，∵a1+a3=30，3S1，2S2，S3成等差数列，
∴ 
=30，3S1+S3=2×2S2，化为：3a2=a3，解得q=3，a1=3．∴an=3n．
（2）解：∵bn+1﹣3bn=3an=3n+1，∴ 
﹣ 
=1．
∴数列 
是等差数列，公差为1，首项为1．
∴ =1+（n﹣1）=n，∴bn=n3n．
∴数列{bn}的前n项和Bn=3+2×32+…+n3n，
3Bn=32+2×33+…+（n﹣1）3n+n3n+1，
∴﹣2Bn=3+32+…+3n﹣n3n+1= 
﹣n3n+1= 
3n+1﹣ 
，
∴Bn= 
×3n+1+ 
（3）解：由题意可得：c2n﹣1=a3n﹣2=33n﹣2，c2n=a3n﹣1=33n﹣1，
∴n=2k（k∈N*）时，c2n﹣1+c2n=33n﹣2+33n﹣1= 
×27n．
Tn=T2k= × 
= 
．
n=2k﹣1时，Tn=T2k﹣1=T2k﹣33n﹣1= ﹣33n﹣1= 
．
因此：n=2k（k∈N*）时， 
= 
= 
+ ∈
．
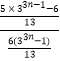n=2k﹣1（k∈N*）时， 
= 
= 
∈ 
．
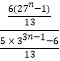综上可得： 
＞ 
．∴a的最大值为
【解析】（1）由a1+a3=30，3S1 ， 2S2 ， S3成等差数列，可得 =30，3S1+S3=2×2S2 ， 化简解出利用等比数列的通项公式即可得出．（2）由bn+1﹣3bn=3an=3n+1 ， 变形为 ﹣ =1，利用等差数列的通项公式可得bn ， 再利用“错位相减法”与等比数列的求和公式可得Bn ． （3）由题意可得：c2n﹣1=a3n﹣2=33n﹣2 ， c2n=a3n﹣1=33n﹣1 ， 可得c2n﹣1+c2n=33n﹣2+33n﹣1= ×27n ． 对n分类讨论即可得出．
【考点精析】通过灵活运用等比数列的通项公式（及其变式）和数列的前n项和，掌握通项公式：
；数列{an}的前n项和sn与通项an的关系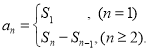
即可以解答此题．
