[题目]若函数y=f(x)图象上存在不同的两点A.B关于y轴对称.则称点对[A.B]是函数y=f(x)的一对“黄金点对 (注:点对[A.B]与[B.A]可看作同一对“黄金点对 )．已知函数f(x)=.则此函数的“黄金点对“有( )A. 0对B. 1对C. 2对D. 3对题目和参考答案——青夏教育精英家教网—

题目内容

【题目】若函数y=f（x）图象上存在不同的两点A，B关于y轴对称，则称点对[A，B]是函数y=f（x）的一对“黄金点对”（注：点对[A，B]与[B，A]可看作同一对“黄金点对”）．已知函数f（x）=，则此函数的“黄金点对“有（　　）

A. 0对B. 1对C. 2对D. 3对

【答案】D

【解析】

根据“黄金点对“，只需要先求出当x＜0时函数f（x）关于y轴对称的函数的解析式，再作出函数的图象，利用两个图象交点个数进行求解即可．

由题意知函数f（x）=2x，x＜0关于y轴对称的函数为，x＞0，

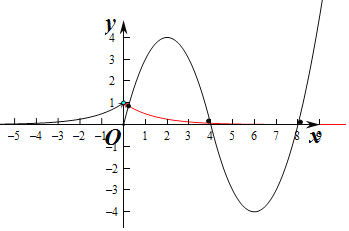
作出函数f（x）和，x＞0的图象，

由图象知当x＞0时，f（x）和y=（）x，x＞0的图象有3个交点．

所以函数f（x）的““黄金点对“有3对．

故选：D．

练习册系列答案

新活力总动员暑系列答案

相关题目

【题目】某企业招聘大学毕业生，经过综合测试，录用了14名女生和6名男生，这20名学生的测试成绩如茎叶图所示(单位：分)，记成绩不小于80分者为等，小于80分者为等．

(1)求女生成绩的中位数及男生成绩的平均数；

(2)如果用分层抽样的方法从等和等中共抽取5人组成“创新团队”，则从等和等中分别抽几人？

(3)在(2)问的基础上，现从该“创新团队”中随机抽取2人，求至少有1人是等的概率．

【题目】已知f（n）=1+ + +…+ （n∈N*），计算得f（2）= ，f（4）＞2，f（8）＞，f（16）＞3，f（32）＞，由此推算：当n≥2时，有（）
A.f（2n）＞（n∈N*）
B.f（2n）＞（n∈N*）
C.f（2n）＞（n∈N*）
D.f（2n）＞（n∈N*）

【题目】在直角坐标系xOy中，圆C的方程为（x+6）2+y2=25．（Ⅰ）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求C的极坐标方程；
（Ⅱ）直线l的参数方程是（t为参数），l与C交与A，B两点，|AB|= ，求l的斜率．

【题目】已知是定义在上的奇函数，且，若对任意的m，，，都有．

若，求a的取值范围．

若不等式对任意和都恒成立，求t的取值范围．

(Ⅰ)应收集多少名女职工样本数据?

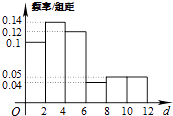
(Ⅱ)根据这300个样本数据,得到职工每周平均上网时间的频率分布直方图(如图所示),其中样本数据分组区间为:，，，，，.试估计该公司职工每周平均上网时间超过4小时的概率是多少?

(Ⅲ)在样本数据中,有70名女职工的每周平均上网时间超过4个小时.请将每周平均上网时间与性别的列联表补充完整,并判断是否有95%的把握认为“该公司职工的每周平均上网时间与性别有关”

【题目】已知函数f（x）=ax2-4ax+1+b（a＞0）的定义域为[2，3]，值域为[1，4]；设g（x）=．

（1）求a，b的值；

（2）若不等式g（2x）-k2x≥0在x∈[1，2]上恒成立，求实数k的取值范围．

【题目】某公司为改善职工的出行条件，随机抽取50名职工，调查他们的居住地与公司的距离d（单位：千米）．若样本数据分组为[0，2]，（2，4]，（4，6]，（6，8]，（8，10]，（10，12]，由数据绘制的分布频率直方图如图所示，则样本中职工居住地与公司的距离不超过4千米的人数为人．

【题目】已知命题p：“方程x2﹣ax+a+3=0有解”，q：“ ﹣a≥0在[0，+∞）上恒成立”，若p或q为真命题，p且q为假命题，求实数a的取值范围．

试题分类