题目内容
11.在平面直角坐标系中,曲线C1的参数方程为 $\left\{\begin{array}{l}{x=acosφ}\\{y=bsinφ}\end{array}\right.$(a>b>0,φ为参数),在以Ο为极点,x轴的正半轴为极轴的坐标系中,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M($\sqrt{3}$,$\frac{1}{2}$)对应的参数φ=$\frac{π}{6}$,射线θ=$\frac{π}{3}$与曲线C2交于点D(1,$\frac{π}{3}$).(1)求曲线C1,C2的直角坐标方程;
(2)若点A(ρ1,θ),Β(ρ2,θ+$\frac{π}{2}$)都在曲线C1上,求$\frac{1}{{ρ}_{1}^{2}+{ρ}_{2}^{2}}$的值.
分析 (1)将M($\sqrt{3}$,$\frac{1}{2}$)对应的参数φ=$\frac{π}{6}$代入$\left\{\begin{array}{l}{x=acosφ}\\{y=bsinφ}\end{array}\right.$消去参数φ可得曲线C1的直角坐标方程;设圆C2的方程为(x-R)2+y2=R2.可得D($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),代入可得R=1,可得C2的直角坐标方程;
(2)可得AB的直角坐标,代入C1的方程可得θ的式子,代入$\frac{1}{{ρ}_{1}^{2}+{ρ}_{2}^{2}}$由三角函数公式可得.
解答 解:(1)将M($\sqrt{3}$,$\frac{1}{2}$)对应的参数φ=$\frac{π}{6}$代入$\left\{\begin{array}{l}{x=acosφ}\\{y=bsinφ}\end{array}\right.$可得$\left\{\begin{array}{l}{\sqrt{3}=acos\frac{π}{6}}\\{\frac{1}{2}=bsin\frac{π}{6}}\end{array}\right.$,
解得a=2,b=1,∴$\left\{\begin{array}{l}{x=2cosφ}\\{y=sinφ}\end{array}\right.$,消去参数φ可得曲线C1的直角坐标方程为$\frac{{x}^{2}}{4}$+y2=1;
设圆C2的半径为R,由题意圆C2的方程为(x-R)2+y2=R2.
由D的极坐标 (1,$\frac{π}{3}$),得D($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),代入(x-R)2+y2=R2,解得R=1,
∴曲线C2的方程为(x-1)2+y2=1.
(2)∵A(ρ1,θ),Β(ρ2,θ+$\frac{π}{2}$)都在曲线C1上,
又点A的直角坐标为(ρ1cosθ,ρ1sinθ),
点B的横坐标为ρ2cos(θ+$\frac{π}{2}$)=-ρ2sinθ,
点B的纵坐标为ρ2sin(θ+$\frac{π}{2}$)=ρ2cosθ,
∴$\frac{{{ρ}_{1}}^{2}co{s}^{2}θ}{4}+{{ρ}_{1}}^{2}si{n}^{2}θ=1$,$\frac{{{ρ}_{2}}^{2}si{n}^{2}θ}{4}+{{ρ}_{2}}^{2}co{s}^{2}θ=1$,
∴$\frac{1}{{ρ}_{1}^{2}+{ρ}_{2}^{2}}$=($\frac{co{s}^{2}θ}{4}+si{n}^{2}θ$)+($\frac{si{n}^{2}θ}{4}+co{s}^{2}θ$)=$\frac{5}{4}$
点评 本题考查参数方程和极坐标方程,化为普通方程是解决问题的关键,属中档题.

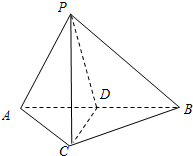 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC. 如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2)、A(x1,y1)、B(x2,y2)均在抛物线上.
如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2)、A(x1,y1)、B(x2,y2)均在抛物线上.