题目内容
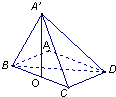 (2009•海淀区二模)如图,矩形ABCD中,AB=2,BC=4,将△ABD沿对角线BD折起到A'BD,使点A'在平面BCD内的射影点O恰好落在BC边上,则异面直线A′B与CD所成角的大小为
(2009•海淀区二模)如图,矩形ABCD中,AB=2,BC=4,将△ABD沿对角线BD折起到A'BD,使点A'在平面BCD内的射影点O恰好落在BC边上,则异面直线A′B与CD所成角的大小为90°
90°
;A'D与平面A'BC所成的角的大小为30°
30°
.分析:由AB∥CD可得∠A′BA即为异面直线A′B与CD所成角,连接A′A,AO,由已知中矩形ABCD中,AB=2,BC=4,点A'在平面BCD内的射影点O恰好落在BC边上,利用勾股定理求出AA′的长度,可求出异面直线A′B与CD所成角的大小;而由由A'O⊥DC,BC⊥DC可得DC⊥平面A'BC,即∠DA′C即为A'D与平面A'BC所成的角,解△DA′C可得答案.
解答:解:由于A'O⊥平面ABCD
∴A'O⊥DC
又∵BC⊥DC,BC∩A'O=O
∴DC⊥平面A'BC
DC⊥A'B
即异面直线A′B与CD所成角的大小为90°
(2)由(1)中DC⊥平面A'BC
即∠DA′C即为A'D与平面A'BC所成的角
在△DA′C中,
∵DC=2,A′D=4,A′C=2
∴∠DA′C=30°
故答案为:90°,30°
∴A'O⊥DC
又∵BC⊥DC,BC∩A'O=O
∴DC⊥平面A'BC
DC⊥A'B
即异面直线A′B与CD所成角的大小为90°
(2)由(1)中DC⊥平面A'BC
即∠DA′C即为A'D与平面A'BC所成的角
在△DA′C中,
∵DC=2,A′D=4,A′C=2
| 3 |
∴∠DA′C=30°
故答案为:90°,30°
点评:本题考查的知识点是直线与平面所成的角,异面直线及其所成的角,其中根据异面直线夹角和线面夹角的定义构造出所求的角,是解答此题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目