题目内容
【题目】已知椭圆![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 在第一象限内的交点是
在第一象限内的交点是![]() ,点
,点![]() 在
在![]() 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 的另一个焦点是
的另一个焦点是![]() ,且
,且![]() .
.
(1) 求椭圆![]() 的方程;
的方程;
(2) 直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 的内切圆面积的最大值.
的内切圆面积的最大值.
【答案】(1) ![]() ;(2)3.
;(2)3.
【解析】试题分析:
(1)由题意求得![]() ,所以椭圆的方程为
,所以椭圆的方程为![]() ;
;
(2)由题意求得内切圆的面积函数: 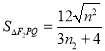 ,换元之后结合对勾函数的性质可得
,换元之后结合对勾函数的性质可得![]() 面积的最大值为3.
面积的最大值为3.
试题解析:
(1)点![]() 在直线
在直线![]() 上,点
上,点![]() 在
在![]() 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆![]() 的右焦点
的右焦点![]()
![]() ,所以
,所以![]() 为
为![]() 又
又![]() ,所以
,所以![]() .
.
又![]() 在椭圆 上,解得
在椭圆 上,解得![]() ,所以椭圆的方程为
,所以椭圆的方程为![]() .
.
(2)由(1)知![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,则
两点,则![]() 的周长为
的周长为![]() ,则
,则![]() (
(![]() 为三角形的内切圆半径),当
为三角形的内切圆半径),当![]() 面积最大时,其内切圆面积最大
面积最大时,其内切圆面积最大
设直线![]() 的方程为:
的方程为: ![]()
由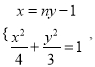 得
得![]()
![]()
所以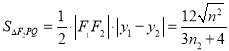
令![]() ,则
,则![]() ,所以
,所以 ,而
,而![]() 在
在![]() 上单调递增,
上单调递增,
所以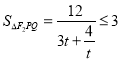 ,当
,当![]() 时取等号,即当
时取等号,即当![]() ,
, ![]() 面积的最大值为3
面积的最大值为3

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目