题目内容
某射手进行射击训练,假设每次射击击中目标的概率为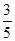 ,且每次射击的结果互不影响,已知射手射击了5
,且每次射击的结果互不影响,已知射手射击了5
次,求:
(1)其中只在第一、三、五次击中目标的概率;
(2)其中恰有3次击中目标的概率.
(1)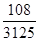 ;(2)
;(2)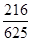 .
.
解析试题分析:(1)由题意可知,该射手在一、三、五次击中目标,在二、四次未击中目标,而每次射击的结果互不影响,因此由概率乘法公式可知所求概率为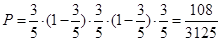 ;(2)该射手射击了
;(2)该射手射击了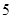 次,其中恰有
次,其中恰有 次击中目标,符合
次击中目标,符合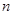 次独立重复试验恰发生
次独立重复试验恰发生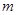 次概率模型,根据二项分布相关内容,可知故所求概率为
次概率模型,根据二项分布相关内容,可知故所求概率为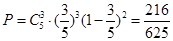 .
.
试题解析:(1)该射手射击了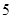 次,其中只在第一、三、五次击中目标,是在确定的情况下击中目标
次,其中只在第一、三、五次击中目标,是在确定的情况下击中目标 次,也即在第二、四次没有击中目标,所以只有一种情况,又各次射击的结果互不影响,
次,也即在第二、四次没有击中目标,所以只有一种情况,又各次射击的结果互不影响,
故所求其概率为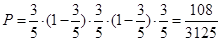 ;
;
(2)该射手射击了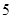 次,其中恰有
次,其中恰有 次击中目标,符合独立重复试验概率模型,
次击中目标,符合独立重复试验概率模型,
故所求其概率为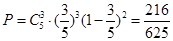 .
.
考点:独立随机事件的概率.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
某工厂生产A,B两种元件,其质量按测试指标划分,指标大于或等于82为正品,小于82为次品.现随机抽取这两种元件各100个进行检测,检测结果统计如下:
| 测试 指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(2)生产1个元件A,若是正品则盈利40元,若是次品则亏损5元;生产1个元件B,若是正品则盈利50元,若是次品则亏损10元.在(1)的前提下,
(ⅰ)X为生产1个元件A和1个元件B所得的总利润,求随机变量X的分布列和数学期望;
(ⅱ)求生产5个元件B所得利润不少于140元的概率.
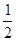 ,乙每次击中目标的概率
,乙每次击中目标的概率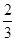 .
.
 分,海选不合格记
分,海选不合格记 分.假设甲、乙、丙海选合格的概率分别为
分.假设甲、乙、丙海选合格的概率分别为 ,他们海选合格与不合格是相互独立的.
,他们海选合格与不合格是相互独立的.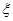 ,求随机变量
,求随机变量 .
.