题目内容
以下茎叶图记录了甲、乙两组各三名同学在期末考试的数学成绩,乙组记录中有一个数字模糊,无法确认.假设这个数字具有随机性,并在图中以a表示.
(1)若甲、乙两个小组的数学平均成绩相同,求a的值;
(2)求乙组平均成绩超过甲组平均成绩的概率;
(3)当a=2时,分别从甲、乙两组中各随机选取一名同学,设这两名同学成绩之差的绝对值为X,求随机变量X的分布列和数学期望,
(1)1;(2)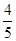 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)根据平均数计算公式 李明在10场篮球比赛中的投篮情况统计如下(假设各场比赛相互独立):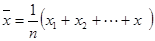 ,直接由甲、乙两个小组的数学平均成绩相等列式求解
,直接由甲、乙两个小组的数学平均成绩相等列式求解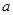 的值;
的值;
(2)分值从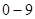 共
共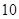 种情况,由(1)中求得的结果可得,当
种情况,由(1)中求得的结果可得,当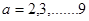 时,乙组平均成绩超过甲组平均成绩,然后由古典概率模型概率计算公式求概率;
时,乙组平均成绩超过甲组平均成绩,然后由古典概率模型概率计算公式求概率;
(3)用枚举法列出所有可能的成绩结果,查出两名同学的数学成绩之差的绝对值为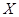 的情况数,然后由古典概率模型概率计算公式求概率,然后列分布列,根据公式
的情况数,然后由古典概率模型概率计算公式求概率,然后列分布列,根据公式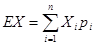 ,此题属于基础题型,关键是读懂题,就能拿满分.
,此题属于基础题型,关键是读懂题,就能拿满分.
试题解析:(1)依题意,得: 
解得 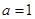 . 3分
. 3分
(2)解:设“乙组平均成绩超过甲组平均成绩”为事件 ,
,
依题意 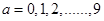 ,共有
,共有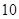 种可能.
种可能.
由(1)可知,当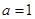 时甲、乙两个小组的数学平均成绩相同,
时甲、乙两个小组的数学平均成绩相同,
所以当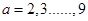 时,乙组平均成绩超过甲组平均成绩,共有
时,乙组平均成绩超过甲组平均成绩,共有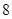 种可能.
种可能.
因此乙组平均成绩超过甲组平均成绩的概率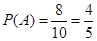 . 7分
. 7分
(3)解:当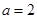 时,分别从甲、乙两组同学中各随机选取一名同学,所有可能的成绩结果有
时,分别从甲、乙两组同学中各随机选取一名同学,所有可能的成绩结果有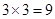 种, 它们是:
种, 它们是: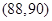 ,
, ,
,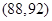 ,
,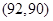 ,
,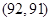 ,
,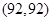 ,
,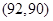 ,
,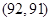 ,
,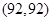
则这两名同学成绩之差的绝对值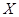 的所有取值为
的所有取值为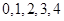
因此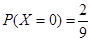 ,
,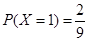 ,
,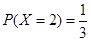 ,
,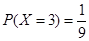 ,
,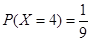 . 10分
. 10分
所以随机变量
0 1 2 3 4 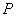
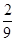
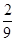

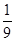
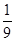
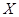 的分布列为:
的分布列为: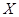

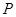

课课练与单元测试系列答案
世纪金榜小博士单元期末一卷通系列答案
单元测试AB卷台海出版社系列答案
黄冈新思维培优考王单元加期末卷系列答案
名校名师夺冠金卷系列答案
小学英语课时练系列答案
培优新帮手系列答案


课堂作业广西教育出版社系列答案
场次 投篮次数 命中次数 场次 投篮次数 命中次数 主场1 22 12 客场1 18 8 主场2 15 12 客场2 13 12 主场3 12 8 客场3 21 7 主场4 23 8 客场4 18 15 主场5 24 20 客场5 25 12
(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过0.6的概率;
(2)从上述比赛中随机选择一个主场和一个客场,求李明的投篮命中率一场超过0.6,一场不超过0.6的概率;
(3)记 为表中10个命中次数的平均数,从上述比赛中随机选择一场,记
为表中10个命中次数的平均数,从上述比赛中随机选择一场,记 为李明在这场比赛中的命中次数,比较
为李明在这场比赛中的命中次数,比较 与
与 的大小(只需写出结论)
的大小(只需写出结论)
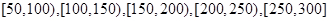 ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.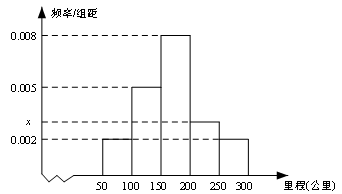
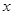 的值;
的值;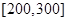 的车辆数;
的车辆数;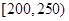 的概率.
的概率.
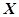 为取得红球的个数.
为取得红球的个数. 表示事件“抽到两 题的编号分别为
表示事件“抽到两 题的编号分别为 ,且
,且 <
< ”.
”.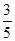 ,且每次射击的结果互不影响,已知射手射击了5
,且每次射击的结果互不影响,已知射手射击了5 两次摸出的球颜色相同的概率是 ;
两次摸出的球颜色相同的概率是 ;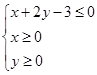 所表示的平面区域内的概率.
所表示的平面区域内的概率.