题目内容
【题目】如图,四边形ABCD是矩形,平面ABCD⊥平面BCE,BE⊥EC.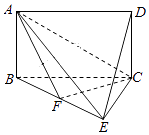
(1)求证:平面AEC⊥平面ABE;
(2)点F在BE上,若DE∥平面ACF,DC=CE= ![]() BC=3,求三棱锥A﹣BCF的体积.
BC=3,求三棱锥A﹣BCF的体积.
【答案】
(1)证明:∵ABCD为矩形,∴AB⊥BC.
∵平面ABCD⊥平面BCE,平面ABCD∩平面BCE=BC,AB平面ABCD,
∴AB⊥平面BCE.
∵CE平面BCE,∴CE⊥AB.
∵CE⊥BE,AB平面ABE,BE平面ABE,AB∩BE=B,
∴CE⊥平面ABE.
∵CE平面AEC,∴平面AEC⊥平面ABE.
(2)解:连接BD交AC于点O,连接OF.
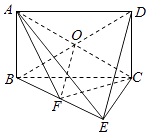
∵DE∥平面ACF,DE平面BDE,平面ACF∩平面BDE=OF,
∴DE∥OF.
又∵矩形ABCD中,O为BD中点,
∴F为BE中点,即BF=FE.
在Rt△BEC中,∵BC=6,EC=3,∴BE= ![]() .
.
∴ ![]() .
.
又AB=DC=3.
∴ ![]() .
.
【解析】1、根据面面垂直的性质定理可得AB⊥平面BCE,即得CE⊥AB,再根据线面垂直的判定定理可得到CE⊥平面ABE,故得到平面AEC⊥平面ABE.
2、由线面平行的性质定理可得DE∥OF,再利用已知可得BF=FE,利用等体积法可求出 V A-BCF.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
