题目内容
4.已知数列{an}满足(n-1)an+1=(n+1)(an-1).(1)求证:数列{$\frac{{a}_{n}}{n}$}是等差数列;
(2)设Sn=$\frac{1}{{a}_{2}-2}$+$\frac{1}{{a}_{3}-3}$+…+$\frac{1}{{a}_{n}-n}$.若a2=6,且nSn<an-1-n2+k对一切n≥2的自然数恒成立,求实数k的取值范围.
分析 (1)由已知得$\frac{{a}_{n+1}}{n+1}$=$\frac{{a}_{n}}{n-1}$-$\frac{1}{n-1}$,令bn=$\frac{{a}_{n}}{(n-1)n}$,推导出bn+1=b2+$\frac{1}{n}$-1,由此能证明数列{$\frac{{a}_{n}}{n}$}是等差数列.
(2)令n=1,得a1=1,从而得到${a}_{n}=2{n}^{2}-n$,$\frac{1}{{a}_{n}-n}$=$\frac{1}{2}(\frac{1}{n-1}-\frac{1}{n})$,由此利用裂项求和法推导出Sn=$\frac{n-1}{2n}$,从而由已知条件得到2n2-11n+7+2k=2(n-$\frac{11}{2}$)2+2k-$\frac{9}{16}$>0对一切n≥2的自然数恒成立,由此能求出实数k的取值范围.
解答 (1)证明:∵数列{an}满足(n-1)an+1=(n+1)(an-1),
∴$\frac{{a}_{n+1}}{n+1}$=$\frac{{a}_{n}}{n-1}$-$\frac{1}{n-1}$
两边同除以n得$\frac{{a}_{n+1}}{n(n+1)}$=$\frac{{a}_{n}}{(n-1)n}$-$\frac{1}{n(n-1)}$,
令bn=$\frac{{a}_{n}}{(n-1)n}$,则bn+1=bn-$\frac{1}{n(n-1)}$=$\frac{1}{n}$-$\frac{1}{n-1}$,
∴bn+1-bn=$\frac{1}{n}$-$\frac{1}{n-1}$,
∴bn-bn-1=$\frac{1}{n-1}$-$\frac{1}{n-2}$,bn-1-bn-2=$\frac{1}{n-2}$-$\frac{1}{n-3}$,…,b3-b2=$\frac{1}{2}$-1,
采用累加法得到bn+1=b2+$\frac{1}{n}$-1,
∴$\frac{{a}_{n}}{n}$=(n-1)bn=(n-1)(b2+$\frac{1}{n-1}$-1)=(n-1)b2+1-(n-1),
$\frac{{a}_{n+1}}{n+1}$=nbn+1=n(b2+$\frac{1}{n}$-1)=nb2+1-n,
∴$\frac{{a}_{n+1}}{n+1}$-$\frac{{a}_{n}}{n}$=b2-1,为常数,
∴数列{$\frac{{a}_{n}}{n}$}是等差数列;
(2)解:∵(n-1)an+1=(n+1)(an-1),a2=6,
令n=1,得2(a1-1)=0,解得a1=1,
∴$\frac{{a}_{1}}{1}=1,\frac{{a}_{2}}{2}=3$,∴$\frac{{a}_{n}}{n}=1+2(n-1)=2n-1$,
∴${a}_{n}=2{n}^{2}-n$,$\frac{1}{{a}_{n}-n}$=$\frac{1}{2}(\frac{1}{n-1}-\frac{1}{n})$,
∴Sn=$\frac{1}{{a}_{2}-2}$+$\frac{1}{{a}_{3}-3}$+…+$\frac{1}{{a}_{n}-n}$=$\frac{1}{2}$(1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{n-1}-\frac{1}{n}$)=$\frac{1}{2}(1-\frac{1}{n})$=$\frac{n-1}{2n}$,
∵nSn<an-1-n2+k对一切n≥2的自然数恒成立,
∴$\frac{n-1}{2}<2(n-1)^{2}-(n-1)-{n}^{2}+k$对一切n≥2的自然数恒成立,
∴2n2-11n+7+2k=2(n-$\frac{11}{4}$)2+2k-$\frac{9}{16}$>0对一切n≥2的自然数恒成立,
∴2k-$\frac{9}{16}$>0,解得k>$\frac{9}{32}$.
∴实数k的取值范围是($\frac{9}{32}$,+∞).
点评 本题考查了分类讨论、等差数列与等比数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案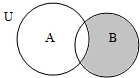
| A. | (CuA)∩B | B. | (CuB)∩A | C. | Cu(A∩B) | D. | Cu(A∪B) |
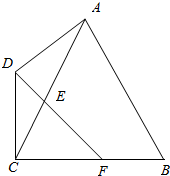 如图所示,平面四边形ABCD中,AB=AC=BC=$\sqrt{3}$,CD=AD=1,已知$\overrightarrow{AE}$=$λ\overrightarrow{AC}$,$\overrightarrow{CF}$=λ$\overrightarrow{CB}$,λ∈(0,1),且存在实数t使$\overrightarrow{CE}$=t$\overrightarrow{CD}$+(1-t)$\overrightarrow{CF}$,则$\overrightarrow{EA}$•$\overrightarrow{AB}$=( )
如图所示,平面四边形ABCD中,AB=AC=BC=$\sqrt{3}$,CD=AD=1,已知$\overrightarrow{AE}$=$λ\overrightarrow{AC}$,$\overrightarrow{CF}$=λ$\overrightarrow{CB}$,λ∈(0,1),且存在实数t使$\overrightarrow{CE}$=t$\overrightarrow{CD}$+(1-t)$\overrightarrow{CF}$,则$\overrightarrow{EA}$•$\overrightarrow{AB}$=( )| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\frac{3}{4}$ | D. | -1 |