题目内容

7．已知函数f（x）=x2+2x+a，f（bx）=9x2-6x+2，其中x∈R，a，b为常数，求方程f（x）=5的根．

分析 由已知中函数f（x）=x2+2x+a，f （bx）=9x-6x+2，我们可以求出参数a，b的值，进而得到方程f（x）=5的根．

解答 解：解：∵f（x）=x2+2x+a，f （bx）=9x-6x+2，
∴（bx）2+2bx+a=9x-6x+2
∴b=-3，a=2
∴方程f（x）=5可化为：x2+2x-3=0，
解得：x=-3，或x=1

点评 本题考查的知识点是根的存在性及根的个数判断，其中根据已知条件，求出a，b的值，是解答本题的关键．

练习册系列答案
相关题目
17．用数学归纳法证明：$\frac{1}{2}$+$\frac{2}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+…+$\frac{n}{{2}^{n}}$=2-$\frac{n+2}{{2}^{n}}$•（n∈N*）
18．已知各项均不相等的正项数列{an}的首项为$\frac{1}{2}$，当n≥2时，an2=an+1•an-1，数列{bn}对任意n∈N+均有（bn+1-bn+2）lga1+（bn+2-bn）lga3+（bn-bn+1）lga5=0．
（1）若a1≠a2，求证：数列{bn}是等差数列；
（2）在（1）的条件下．已知b1=2，b4=5，a2=$\frac{1}{2}$a1，数列{cn}满足cn=an•bn，记数列{cn}的前n项和为Sn，求证：Sn＜3．
15．设集合A={x|2x＜4}，B={x|m2＜x＜m2+1}，若“x∈A”是“x∈B”的必要不充分条件，求m的取值范围．
2．探究：比较下面几个例子．你发现两个集合之间有哪几种基本关系？
A={3，6，9}与B={x|x=3k，k∈N且k≤333}；
C={茶陵二中学生}与D={茶陵二中高一学生}；
E={x|x（x-1）（x-2）=0}与F={0，1，2}．
4．已知数列{an}满足（n-1）an+1=（n+1）（an-1）．
（1）求证：数列{$\frac{{a}_{n}}{n}$}是等差数列；
（2）设Sn=$\frac{1}{{a}_{2}-2}$+$\frac{1}{{a}_{3}-3}$+…+$\frac{1}{{a}_{n}-n}$．若a2=6，且nSn＜an-1-n2+k对一切n≥2的自然数恒成立，求实数k的取值范围．
11．已知函数f（x）=x2+mx+n的图象过点（1，3），且f（-1+x）=f（-1-x）对任意实数都成立，函数y=g（x）与y=f（x）的图象关于原点对称．
（1）求f（x）与g（x）的解析式；
（2）若F（x）=g（x）-λf（x）在[-1，1]上是增函数，求实数λ的取值范围．
8．如图，四边形ABCD是边长为1的正方形，延长CD至E，使得DE=2CD，动点P从点A出发，沿正方形的边按逆时针方向运动到C点，$\overrightarrow{AP}$=$λ\overrightarrow{AB}$+μ$\overrightarrow{AE}$，若$\overrightarrow{AE}$•$\overrightarrow{AP}$=-$\frac{5}{3}$，则λ+μ=（　　）
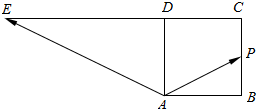
A．$\frac{5}{6}$B．1或2C．$\frac{5}{6}$或2D．1或$\frac{5}{6}$
9．画出下列函数的图象：
F（x）=$\left\{\begin{array}{l}{0，x≤0}\\{1，x＞0}\end{array}\right.$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网