Question

【题目】在边长为2的菱形中，，将菱形沿对角线对折，使二面角的余弦值为，则所得三棱锥的内切球的表面积为（ ）

A. B. C. D.

Answer 1

【答案】C

【解析】

作出图形，利用菱形对角线相互垂直的性质得出DN⊥AC，BN⊥AC，可得出二面角B﹣AC﹣D的平面角为∠BND，再利用余弦定理求出BD，可知三棱锥B﹣ACD为正四面体，可得出内切球的半径R，再利用球体的表面积公式可得出答案．

如下图所示，

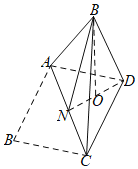
易知△ABC和△ACD都是等边三角形，取AC的中点N，则DN⊥AC，BN⊥AC．

所以，∠BND是二面角B﹣AC﹣D的平面角，过点B作BO⊥DN交DN于点O，可得BO⊥平面ACD．

因为在△BDN中，，所以，BD2＝BN2+DN2﹣2BNDNcos∠BND，

则BD＝2．

故三棱锥A﹣BCD为正四面体，则其内切球半径为正四面体高的，又正四面体的高为棱长的，故．

因此，三棱锥A﹣BCD的内切球的表面积为．

故选：C．