题目内容
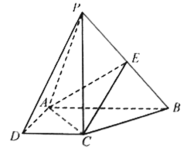
【题目】一幅标准的三角板如图（1）中，
为直角，
，
为直角，
，且
，把
与
拼齐使两块三角板不共面，连结
如图（2）.
（1）若
是
的中点，求证：
；
（2）在《九章算术》中，称四个面都是直角三角形的三棱锥为“鳖臑”，若图（2）中
，三棱锥
的体积为
，则图（2）是否为鳖臑？说明理由.
【答案】（1）见解析；（2）见解析
【解析】
（1）取
的中点
，连接
，通过证明直线
平面
，证得直线
.（2）根据
的长度，求得
的长度，求得三角形
的面积，利用体积公式后求得三棱锥的高为
，由此证得
平面，进而证得四个三角形都是直角三角形.
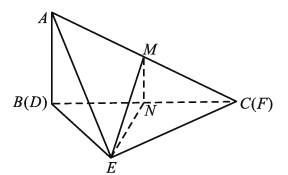
（1）证明：设中点为，连结，
∵
，
，
∴
，
∵
，
，
，
∴
∵
，
∴平面，
故
；
（2）此时三棱锥
时鳖臑
∵
，
又三棱锥的体积
高
，
所以平面，
那么，在三棱锥中，
显然是直角，
∵
，
，
平面
也是直角
那么，该三棱锥的四个面都是直角三角形，所以它是鳖臑.
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
【题目】某城市理论预测2020年到2024年人口总数与年份的关系如下表所示：
年份202x（年） | 0 | 1 | 2 | 3 | 4 |
人口数y（十万） | 5 | 7 | 8 | 11 | 19 |
（1）请在右面的坐标系中画出上表数据的散点图；
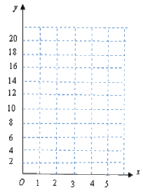
（2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程；
（3）据此估计2025年该城市人口总数.
（参考公式：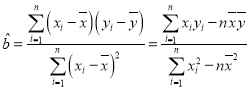
，
）
