题目内容
5.已知甲、乙两名篮球运动员每次投篮命中的概率分别为$\frac{1}{2}$、p,甲、乙每次投篮是否投中相互之间没有影响,乙投篮3次均未命中的概率为$\frac{1}{27}$.(1)求p的值;
(2)若甲投篮1次、乙投篮2次,两人投篮命中的次数的和记为X,求X的分布列和数学期望E(X)
分析 (1)服从B(3,p)独立重复试验,利用概率公式求解即可.
(2)确定X=0,1,2,3,分析得出当x=0时,甲,乙两人投篮命中次数都为0,当x=1时,甲,乙两人投篮命中次数为0,1或1,0;当x=2时,甲,乙两人投篮命中次数为1,1.或0,2;当x=3时,甲,乙两人投篮命中次数为1,2;利用独立事件同时发生的概率求解即可.
解答 解:(1)服从B(3,p)独立重复试验
根据题意得出:${C}_{3}^{3}$p3(1-P)0=$\frac{1}{27}$,
∴p=$\frac{1}{3}$,
(2)X=0,1,2,3
当x=0时,甲,乙两人投篮命中次数都为0,
P(X=0)=(1-$\frac{1}{2}$)×${C}_{2}^{2}$(1-$\frac{1}{3}$)2=$\frac{2}{9}$,
当x=1时,甲,乙两人投篮命中次数为0,1或1,0.
P(X=1)=(1-$\frac{1}{2}$)×${C}_{2}^{1}$×$\frac{1}{3}$×(1-$\frac{1}{3}$)+$\frac{1}{2}×$${C}_{2}^{2}$(1-$\frac{1}{3}$)2=$\frac{2}{9}$$+\frac{2}{9}$=$\frac{4}{9}$,
当x=2时,甲,乙两人投篮命中次数为1,1.或0,2
P(X=2)=$\frac{1}{2}$×${C}_{2}^{1}$×$\frac{1}{3}$×(1-$\frac{1}{3}$)+(1-$\frac{1}{2}$)×${C}_{2}^{2}$($\frac{1}{3}$)2=$\frac{2}{9}$$+\frac{1}{18}$=$\frac{5}{18}$,
当x=3时,甲,乙两人投篮命中次数为1,2.
P(X=3)=$\frac{1}{2}×$($\frac{1}{3}$)2=$\frac{1}{18}$,
| X | 0 | 1 | 2 | 3 |
| P | $\frac{2}{9}$ | $\frac{4}{9}$ | $\frac{5}{18}$ | $\frac{1}{18}$ |
点评 本题考查了离散型的概率求解,分布列,数学期望,考查了学生的阅读分析问题的能力,计算能力,属于中档题.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案| A. | $\frac{1}{10}$ | B. | $\frac{1}{300}$ | C. | $\frac{1}{2500}$ | D. | $\frac{1}{3000}$ |
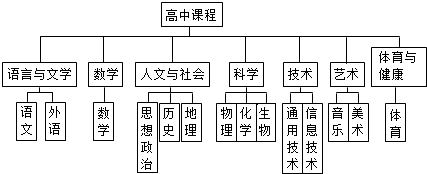
| A. | 艺术 | B. | 人文与社会 | C. | 技术 | D. | 科学 |
| A. | -$\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | 3 | D. | 3+3$\sqrt{2}$ |
| A. | 所有实数的平方都不是正数 | B. | 有的实数的平方是正数 | ||
| C. | 至少有一个实数的平方不是正数 | D. | 至少有一个实数的平方是正数 |
| A. | (-∞,1) | B. | [-2,0] | C. | (-2-2$\sqrt{2}$,-2+2$\sqrt{2}})$) | D. | [0,1] |
 如图,点A是单位圆与x轴正半轴的交点,点B是单位圆上一个定点,点P是一个动点,且∠AOB=120°,∠AOP=θ(0<θ<π),$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.
如图,点A是单位圆与x轴正半轴的交点,点B是单位圆上一个定点,点P是一个动点,且∠AOB=120°,∠AOP=θ(0<θ<π),$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.