题目内容
已知椭圆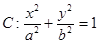 的短轴长等于焦距,椭圆C上的点到右焦点
的短轴长等于焦距,椭圆C上的点到右焦点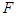 的最短距离为
的最短距离为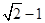 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点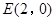 且斜率为
且斜率为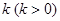 的直线
的直线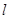 与
与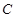 交于
交于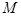 、
、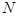 两点,
两点,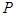 是点
是点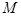 关于
关于 轴的对称点,证明:
轴的对称点,证明: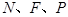 三点共线.
三点共线.
(Ⅰ) 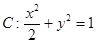 ; (Ⅱ)证明
; (Ⅱ)证明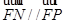 得出
得出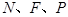 三点共线
三点共线
解析试题分析:(Ⅰ)由题可知: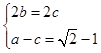 …………2分
…………2分
解得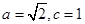 ,
,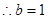
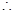 椭圆C的方程为
椭圆C的方程为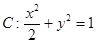 …………………………4分
…………………………4分
(Ⅱ)设直线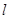 :
: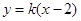 ,
,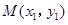 ,
,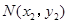 ,
,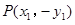 ,
,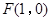 ,
,
由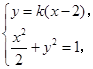 得
得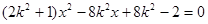 .…………6分
.…………6分
所以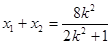 ,
,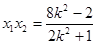 . ……………………8分
. ……………………8分
而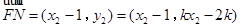 ,
,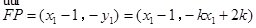 ,10分
,10分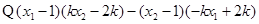
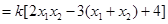
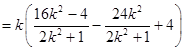
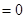
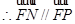
∴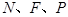 三点共线 ……………………………………12分
三点共线 ……………………………………12分
考点:本题主要考查椭圆标准方程,直线与椭圆的位置关系。
点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题求椭圆标准方程时,主要运用了椭圆的定义及几何性质。为证明三点共线,本题利用了平面向量共线的条件,运用向量的坐标运算,简化了解题过程。

练习册系列答案
相关题目
 ,
, 为直线
为直线 上任意一点,过
上任意一点,过 .
.
 三点的横坐标成等差数列;
三点的横坐标成等差数列; 时,
时, .求此时抛物线的方程。
.求此时抛物线的方程。 (a>b>0)的右焦点为F
(a>b>0)的右焦点为F (1,0),离心率为
(1,0),离心率为 ,P为左顶点。
,P为左顶点。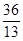 ,求直线AB的方程。
,求直线AB的方程。 与曲线
与曲线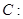

 交于不同的两点
交于不同的两点 ,
, 为坐标原点.
为坐标原点. ,求证:曲线
,求证:曲线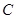 是一个圆;
是一个圆; ,当
,当 且
且 时,求曲线
时,求曲线 的取值范围.
的取值范围. 为抛物线
为抛物线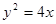 的焦点,
的焦点,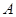 为抛物线上任意一点,已
为抛物线上任意一点,已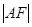 为半径画圆,与
为半径画圆,与 轴负半轴交于
轴负半轴交于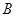 点,试判断过
点,试判断过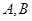 的直线与抛物线的位置关系,并证明。
的直线与抛物线的位置关系,并证明。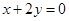 与圆
与圆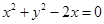 的交点为A、B,
的交点为A、B,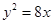 的焦点,M的离心率
的焦点,M的离心率 ,过M的右焦点F作不与坐标轴垂直的直线
,过M的右焦点F作不与坐标轴垂直的直线 ,交M于A,B两点。
,交M于A,B两点。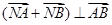 ,求实数t的取值范围。
,求实数t的取值范围。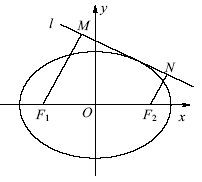
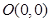 的距离是到定点
的距离是到定点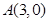 距离的二倍,求这条曲线的方程.
距离的二倍,求这条曲线的方程.