题目内容
(本小题满分12分)
已知函数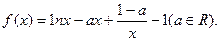
(Ⅰ)当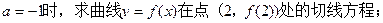
(Ⅱ)当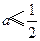 时,讨论
时,讨论 的单调性.
的单调性.
已知函数
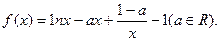
(Ⅰ)当
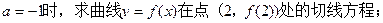
(Ⅱ)当
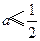 时,讨论
时,讨论 的单调性.
的单调性.(Ⅰ)
( Ⅱ )当 时,函数
时,函数 在(0,1)上单调递减;
在(0,1)上单调递减;
函数 在 (1,+∞) 上单调递增
在 (1,+∞) 上单调递增
当 时,函数
时,函数 在(0,+∞)上单调递减
在(0,+∞)上单调递减
当 时,函数
时,函数 在(0,1)上单调递减;
在(0,1)上单调递减;
函数 在
在 上单调递增;
上单调递增;
函数 在(
在( ,+∞)上单调递减。
,+∞)上单调递减。

( Ⅱ )当
 时,函数
时,函数 在(0,1)上单调递减;
在(0,1)上单调递减;函数
 在 (1,+∞) 上单调递增
在 (1,+∞) 上单调递增当
 时,函数
时,函数 在(0,+∞)上单调递减
在(0,+∞)上单调递减当
 时,函数
时,函数 在(0,1)上单调递减;
在(0,1)上单调递减;函数
 在
在 上单调递增;
上单调递增;函数
 在(
在( ,+∞)上单调递减。
,+∞)上单调递减。本题考查了导数的运算、导数的几何意义、直线方程的求解以及利用导数讨论函数的单调性,考查了学生利用导数知识解决函数问题的能力以及分类讨论与等价转化的数学思想。
解:(Ⅰ)当

所以
因此,
即 曲线 ……………………
……………………
又
所以曲线
(Ⅱ)因为 ,
,
所以

 ,
,
令

(1) 当 时,
时, ,
, ,
,
所以 当 时,
时, ,此时
,此时 ,函数
,函数 单调递减;
单调递减;
当 函数
函数
(2) 当 时,由
时,由 ,
,
即 解得
解得
①当 时,
时, ,
, 恒成立,此时
恒成立,此时 ,函数
,函数 f在
f在 上单调递减;
上单调递减;
②当 时,
时,
 时,
时, ,此时
,此时 ,函数
,函数 单调递减
单调递减
 时,
时, ,此时
,此时 ,函数
,函数 单调递增
单调递增
 时,
时, ,此时
,此时 ,函数
,函数 单调递减
单调递减
③当 时,由于
时,由于 ,
,
 时,
时, ,此时
,此时 函数
函数 单调递减;
单调递减;
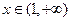 时,
时, 此时函数
此时函数 单调递增。
单调递增。
综上所述:
当 时,函数
时,函数 在(0,1)上单调递减;
在(0,1)上单调递减;
函数 在 (1,+∞) 上单调递增
在 (1,+∞) 上单调递增
当 时,函数
时,函数 在(0,+∞)上单调递减
在(0,+∞)上单调递减
当 时,函数
时,函数 在(0,1)上单调递减;
在(0,1)上单调递减;
函数 在
在 上单调递增;
上单调递增;
函数 在(
在( ,+∞)上单调递减。
,+∞)上单调递减。
解:(Ⅰ)当


所以

因此,

即 曲线
 ……………………
……………………又

所以曲线

(Ⅱ)因为
 ,
,所以


 ,
,令


(1) 当
 时,
时, ,
, ,
,所以 当
 时,
时, ,此时
,此时 ,函数
,函数 单调递减;
单调递减;当
 函数
函数
(2) 当
 时,由
时,由 ,
,即
 解得
解得
①当
 时,
时, ,
, 恒成立,此时
恒成立,此时 ,函数
,函数 f在
f在 上单调递减;
上单调递减;②当
 时,
时,
 时,
时, ,此时
,此时 ,函数
,函数 单调递减
单调递减 时,
时, ,此时
,此时 ,函数
,函数 单调递增
单调递增 时,
时, ,此时
,此时 ,函数
,函数 单调递减
单调递减③当
 时,由于
时,由于 ,
, 时,
时, ,此时
,此时 函数
函数 单调递减;
单调递减;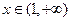 时,
时, 此时函数
此时函数 单调递增。
单调递增。综上所述:
当
 时,函数
时,函数 在(0,1)上单调递减;
在(0,1)上单调递减;函数
 在 (1,+∞) 上单调递增
在 (1,+∞) 上单调递增当
 时,函数
时,函数 在(0,+∞)上单调递减
在(0,+∞)上单调递减当
 时,函数
时,函数 在(0,1)上单调递减;
在(0,1)上单调递减;函数
 在
在 上单调递增;
上单调递增;函数
 在(
在( ,+∞)上单调递减。
,+∞)上单调递减。
练习册系列答案
相关题目
 在点
在点 处的切线方程为( )
处的切线方程为( ) B
B C
C D
D 
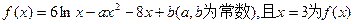 的一个极值点.
的一个极值点.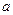 ;
;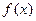 的单调区间;
的单调区间;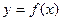 的图象与x轴有且只有3个交点,求b的取值范围.
的图象与x轴有且只有3个交点,求b的取值范围.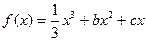 (b、c为常数)的两个极值点分别为
(b、c为常数)的两个极值点分别为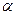 、
、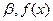 在点
在点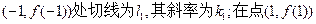 处的切线为l2,其斜率为k2。
处的切线为l2,其斜率为k2。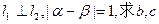 ;
;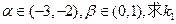 的取值范围。
的取值范围。
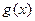 的单调递增区间;
的单调递增区间;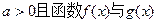 的图像有公共点,且在该点处的切线相同,用a表示b,并求b的最大值。
的图像有公共点,且在该点处的切线相同,用a表示b,并求b的最大值。 =6,则x0=( )
=6,则x0=( )







 ,则
,则 =_______
=_______ 是
是 的导函数,则
的导函数,则 的值是 .
的值是 .