题目内容
17.在平面区域D:|a+2|+|b-2|≤2上任取一点(a,b),则有序实数对(a,b)满足一元二次方程ax2+bx+2=0有一根在(-1,0),另一根在(1,2)条件的概率为$\frac{2}{3}$.分析 确定平面区域,求出面积,以面积的比求出概率.
解答 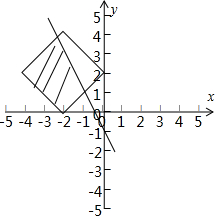 解:平面区域D:|a+2|+|b-2|≤2,如图所示,面积为8,
解:平面区域D:|a+2|+|b-2|≤2,如图所示,面积为8,
∵有序实数对(a,b)满足一元二次方程ax2+bx+2=0有一根在(-1,0),另一根在(1,2),
∴2(a-b+2)<0,(a+b+2)(4a+2b+2)<0,区域如图阴影,面积为$\frac{\sqrt{2}+\frac{5}{3}\sqrt{2}}{2}×2\sqrt{2}$=$\frac{16}{3}$
∴所求的概率为$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题考查概率的计算,考查平面图形的作法,正确求面积是关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
7.下列命题中正确的是( )
| A. | 两两相交的三条直线共面 | |
| B. | 两条相交直线上的三个点可以确定一个平面 | |
| C. | 梯形是平面图形 | |
| D. | 一条直线和一个点可以确定一个平面 |
8.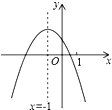 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
①4ac-b2<0;
②4a+c<2b;
③3b+2c<0;
④m(am+b)+b<a(m≠-1),
其中正确结论的个数是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac-b2<0;
②4a+c<2b;
③3b+2c<0;
④m(am+b)+b<a(m≠-1),
其中正确结论的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
7.根据历年气象资料统计,蚌埠地区五月份刮东风的概率是$\frac{4}{15}$,既刮东风又下雨的概率是$\frac{7}{30}$,那么在“五月份刮东风”的条件下,蚌埠地区五月份下雨的概率是( )
| A. | $\frac{1}{30}$ | B. | $\frac{1}{2}$ | C. | $\frac{56}{900}$ | D. | $\frac{7}{8}$ |