题目内容
2.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x-1.(1)求f(2)+f(-1)的值;
(2)求f(x)在R上的解析式.
分析 (1)根据函数奇偶性的关系以及函数的表达式即可求f(2)+f(-1)的值;
(2)根据函数奇偶性的性质,利用对称性进行求解即可.
解答 解:(1)∵f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x-1,
∴f(2)+f(-1)=f(2)-f(1)=22+2×2-1-(2+2-1)=10;
(2)若x<0,则-x>0,即f(-x)=2-x-2x-1,
∵f(x)为定义在R上的奇函数,
∴f(-x)=-f(x),
即f(-x)=2-x-2x-1=-f(x),
则f(x)=-2-x+2x+1,x<0,
则f(x)在R上的解析式为f(x)=$\left\{\begin{array}{l}{{2}^{x}+2x-1,}&{x≥0}\\{-{2}^{-x}+2x+1,}&{x<0}\end{array}\right.$.
点评 本题主要考查函数值和函数解析式的求解,利用函数奇偶性的性质是解决本题的关键.

练习册系列答案
相关题目
10.已知f(x)=$\left\{\begin{array}{l}{a}^{x},x<0\\(a-3)x+4a,x≥0\end{array}\right.$满足对任意x1≠x2,都有[f(x1)-f(x2)](x1-x2)<0成立,则a的取值范围是( )
| A. | $({0,\frac{1}{4}}]$ | B. | (0,1) | C. | $[{\frac{1}{4},1})$ | D. | (0,3) |
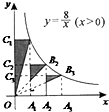 如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{8}{x}({x>0})$的图象分别交于点B1、B2、B3,分别过点B1,B2,B3作x轴的平行线,分别与y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为$\frac{49}{9}$.
如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=$\frac{8}{x}({x>0})$的图象分别交于点B1、B2、B3,分别过点B1,B2,B3作x轴的平行线,分别与y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为$\frac{49}{9}$.