题目内容
【题目】函数①
；②
；③
；④
；其中对于
定义域内任意一个自变量
都存在唯一自变量
，使得
成立的函数是（）
A.①③B.②③C.①②④D.③
【答案】D
【解析】
根据题意可知其中对于f（x）定义域内的任意一个自变量x1都存在唯一个自变量x2，使
3即要判断对于任意一个自变量x，即函数在定义域内每个函数值，都有其倒数的9倍，从而得到结论．
在①f(x)=3lnx中,∵f(1)=0,∴不存在自变量
,使
成立，故①不成立；
在②f(x)=3ecosx中，∵函数不是单调函数，
∴对于定义域内的任意一个自变量
，使成立的自变量不唯一，故②不成立；
在③
中，函数是单调函数，且函数值不为0，
故定义域内的任意一个自变量都存在唯一一个自变量,使成立，故③成立；
在④f(x)=3cosx中,∵f(
)=0,∴不存在自变量,使成立，故④不成立。
故选：D.
练习册系列答案
相关题目
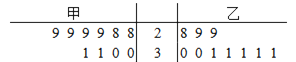
【题目】某家具公司生产甲、乙两种书柜，制柜需先制白胚再油漆，每种柜的制造白胚工时数、油漆工时数的有关数据如下：
工艺要求 | 产品甲 | 产品乙 | 生产能力（工时/天） |
制白胚工时数 | 6 | 12 | 120 |
油漆工时数 | 8 | 4 | 64 |
单位利润 | 20元 | 24元 |
则该公司合理安排这两种产品的生产，每天可获得的最大利润为______.
