题目内容

18．设f（x）=x（x-1）（x-2）…（x-99），则f′（0）=-99!．

分析 把x看作一项，后99个因式的乘积看作另一项，利用积的导数公式进行求解即可得到答案．

解答 解：∵f（x）=x（x-1）（x-2）…（x-99）=x[（x-1）（x-2）…（x-99）]，
∴f′（x）=x′[（x-1）（x-2）…（x-99）]+x[（x-1）（x-2）…（x-99）]′
=[（x-1）（x-2）…（x-99）]+x[（x-1）（x-2）…（x-99）]′，
∴f′（0）=[（-1）×（-2）×…•×（-99）]+0×[（x-1）（x-2）…（x-99）]′=-99!．
故答案为：-99!．

点评 本题主要考查导数的基本运算，将函数分解为两部分，利用积的导数公式是解决本题的关键，是基础题．

练习册系列答案
相关题目
4．化简：$\frac{1+i}{1-i}$+$\frac{1-i}{1+i}$．
9．已知奇函数f（x）=$\frac{m-g（x）}{1+g（x）}$的定义域为R，其中g（x）为指数函数且过点（2，9）．
（Ⅰ）求函数y=f（x）的解析式；
（Ⅱ）判断函数f（x）的单调性，并用函数单调性定义证明．
6．设0＜b＜1+a，若关于x的不等式（x-b）2＞（ax）2的解集中的整数解恰有3个，则（　　）
A．-1＜a＜0B．0＜a＜1C．1＜a＜3D．3＜a＜6
13．在等比数列{an}中，若a3a5a7a9a11=243，则a7=（　　）
A．9B．1C．2D．3
3．极坐标系与直角坐标系xoy有相同的长度单位，以原点为极点，以x铀正半轴为极轴，已知曲线C1的极坐标方程为ρ=4cosθ，直线l的参数方程为$\left\{{\begin{array}{l}{x=-2+\frac{1}{2}t}\\{y=\frac{{\sqrt{3}}}{2}t}\end{array}}\right.$（t为参数），射线$θ=φ，θ=φ+\frac{π}{4}，θ=φ-\frac{π}{4}$与曲线C1交于（不包括极点O）三点A、B、C．
（Ⅰ）求曲线C1化成直角坐标方程及直线l的普通方程，并求曲线C1上的点到直线l的最小值．
（Ⅱ） 求证：$|{OB}|+|{OC}|=\sqrt{2}|{OA}|$．
10．执行如图所示的程序框图，若输入x=7，y=6，则输出的有序数对为（　　）
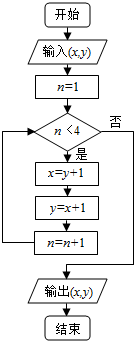
A．（11，12）B．（12，13）C．（13，14）D．（13，12）
7．已知Rt△ABC中，两直角边长为方程x2-（2m+7）x+4m（m-2）=0的两根，且斜边长为13，求S△ABC的值．
8．在△ABC中，若sin（A-B）=0，则三角形是等腰三角形．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网