题目内容
在平面直角坐标系xOy中,椭圆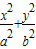 =1(a>b>0)的焦点为 F1(-1,0),F2(1,0),左、右顶点分别为A,B,离心率为
=1(a>b>0)的焦点为 F1(-1,0),F2(1,0),左、右顶点分别为A,B,离心率为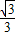 ,动点P到F1,F2的距离的平方和为6.
,动点P到F1,F2的距离的平方和为6.(1)求动点P的轨迹方程;
(2)若
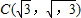 ,
, ,Q为椭圆上位于x轴上方的动点,直线DM•CN,BQ分别交直线m于点M,N.
,Q为椭圆上位于x轴上方的动点,直线DM•CN,BQ分别交直线m于点M,N.(i)当直线AQ的斜率为
 时,求△AMN的面积;
时,求△AMN的面积;(ii)求证:对任意的动点Q,DM•CN为定值.
【答案】分析:(1)利用动点P到F1,F2的距离的平方和为6,建立方程,化简可得P的轨迹方程;
(2)确定椭圆的方程,求出M、N的坐标,( i)当直线AQ的斜率为 时,直线方程与椭圆方程联立,表示出三角形的面积,即可求△AMN的面积;(ii)表示出DM,CN,计算DM•CN,可得定值.
时,直线方程与椭圆方程联立,表示出三角形的面积,即可求△AMN的面积;(ii)表示出DM,CN,计算DM•CN,可得定值.
解答: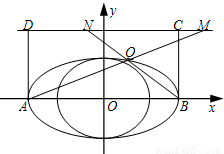 (1)解:设P(x,y),则
(1)解:设P(x,y),则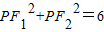 ,
,
即(x+1)2+y2+(x-1)2+y2=6,整理得,x2+y2=2,
所以动点P的轨迹方程为x2+y2=2.…(4分)
(2)解:由题意知,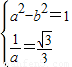 ,解得
,解得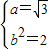 ,
,
所以椭圆方程为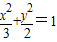 . …(6分)
. …(6分)
则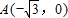 ,
,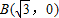 ,设Q(x,y),y>0,则
,设Q(x,y),y>0,则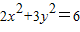 ,
,
直线AQ的方程为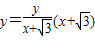 ,令
,令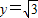 ,得
,得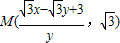 ,
,
直线BQ的方程为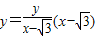 ,令
,令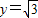 ,得
,得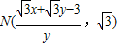 ,
,
( i)当直线AQ的斜率为 时,有
时,有 ,消去x并整理得,
,消去x并整理得,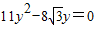 ,解得
,解得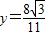 或y=0(舍),…(10分)
或y=0(舍),…(10分)
所以△AMN的面积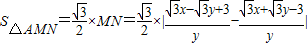 =
=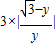 =
= . …(12分)
. …(12分)
(ii)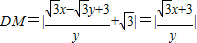 ,
,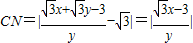 ,
,
所以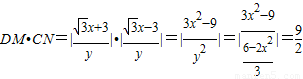 .
.
所以对任意的动点Q,DM•CN为定值,该定值为 . …(16分)
. …(16分)
点评:本题考查轨迹方程,考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形面积的计算,考查学生的计算能力,综合性强.
(2)确定椭圆的方程,求出M、N的坐标,( i)当直线AQ的斜率为
 时,直线方程与椭圆方程联立,表示出三角形的面积,即可求△AMN的面积;(ii)表示出DM,CN,计算DM•CN,可得定值.
时,直线方程与椭圆方程联立,表示出三角形的面积,即可求△AMN的面积;(ii)表示出DM,CN,计算DM•CN,可得定值.解答:
 (1)解:设P(x,y),则
(1)解:设P(x,y),则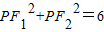 ,
,即(x+1)2+y2+(x-1)2+y2=6,整理得,x2+y2=2,
所以动点P的轨迹方程为x2+y2=2.…(4分)
(2)解:由题意知,
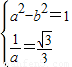 ,解得
,解得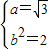 ,
,所以椭圆方程为
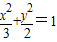 . …(6分)
. …(6分)则
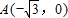 ,
,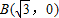 ,设Q(x,y),y>0,则
,设Q(x,y),y>0,则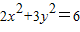 ,
,直线AQ的方程为
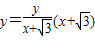 ,令
,令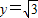 ,得
,得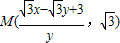 ,
,直线BQ的方程为
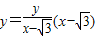 ,令
,令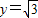 ,得
,得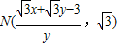 ,
,( i)当直线AQ的斜率为
 时,有
时,有 ,消去x并整理得,
,消去x并整理得,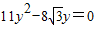 ,解得
,解得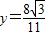 或y=0(舍),…(10分)
或y=0(舍),…(10分)所以△AMN的面积
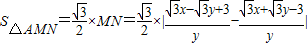 =
=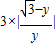 =
= . …(12分)
. …(12分)(ii)
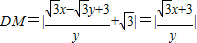 ,
,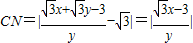 ,
,所以
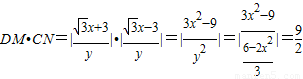 .
.所以对任意的动点Q,DM•CN为定值,该定值为
 . …(16分)
. …(16分)点评:本题考查轨迹方程,考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形面积的计算,考查学生的计算能力,综合性强.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是