题目内容
直角坐标平面xoy中,若定点A(1,2)与动点P(x,y)满足| OP |
| OA |
分析:设点P(x,y),根据点P和A的坐标,进而可得
和
,再代入
•
=4,答案可得.
| OP |
| OA |
| OP |
| OA |
解答:解:设点P(x,y),则
=(x,y)
因为A(1,2)
所以
=(1,2)
因为
•
=4,
所以(x,y)•(1,2)=4
即x+2y=4,
即x+2y-4=0
故答案为:x+2y-4=0
| OP |
因为A(1,2)
所以
| OA |
因为
| OP |
| OA |
所以(x,y)•(1,2)=4
即x+2y=4,
即x+2y-4=0
故答案为:x+2y-4=0
点评:本题主要考查了利用向量的关系求点的轨迹方程.属基础题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
在直角坐标平面xOy中,已知点A(3,2),点B在圆x2+y2=1上运动,动点P满足
=
,则点P的轨迹是( )
| AP |
| PB |
| A、圆 | B、椭圆 | C、抛物线 | D、直线 |
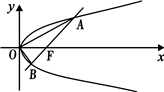 过直角坐标平面xOy中的抛物线y2=2px(p>0)的焦点F作一条倾斜角为
过直角坐标平面xOy中的抛物线y2=2px(p>0)的焦点F作一条倾斜角为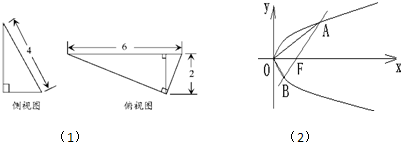
 (2005•上海模拟)本题共有2个小题,第1小题满分8分,第2小题满分6分
(2005•上海模拟)本题共有2个小题,第1小题满分8分,第2小题满分6分