题目内容
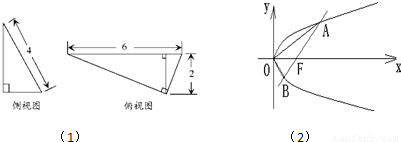
(1)某三棱锥的侧视图和俯视图如图所示,求三棱锥的体积.
(2)过直角坐标平面xOy中的抛物线y2=2px(p>0)的焦点F作一条倾斜角为
的直线与抛物线相交于A,B两点.用p表示A,B之间的距离.
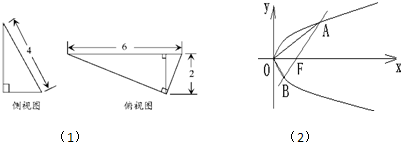
(2)过直角坐标平面xOy中的抛物线y2=2px(p>0)的焦点F作一条倾斜角为
| π | 4 |

分析:(1)由三棱锥的侧视图和俯视图,先求出该三棱锥的高,由此能求出其体积.
(2)焦点F(1,0),过抛物线的焦点且倾斜角为
的直线方程是y=x-
,由
,得x2-3px+
=0,由此能用p表示A,B之间的距离.
(2)焦点F(1,0),过抛物线的焦点且倾斜角为
| π |
| 4 |
| p |
| 2 |
|
| p2 |
| 4 |
解答:解:(1)由三棱锥的侧视图和俯视图,
知该三棱锥的高h=
=
=2
,
∴V=
×
×6×2×2
=4
.
(2)焦点F(1,0),过抛物线的焦点且倾斜角为
的直线方程是y=x-
,
由
,得x2-3px+
=0,
∴xA+xB=3p,xAxB=
,
∴|AB|=xA+xB+p=4p.
知该三棱锥的高h=
| 42-22 |
| 12 |
| 3 |
∴V=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
(2)焦点F(1,0),过抛物线的焦点且倾斜角为
| π |
| 4 |
| p |
| 2 |
由
|
| p2 |
| 4 |
∴xA+xB=3p,xAxB=
| p2 |
| 4 |
∴|AB|=xA+xB+p=4p.
点评:第(1)考查三棱锥的体积的求法,第(2)题考查抛物线的焦点弦的求法.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
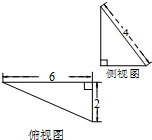 某三棱锥的侧视图和俯视图如图所示,则该三棱锥的体积为
某三棱锥的侧视图和俯视图如图所示,则该三棱锥的体积为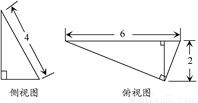
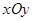 中的抛物线
中的抛物线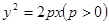 的焦点
的焦点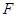 作一条倾斜角为
作一条倾斜角为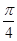 的直线与抛物线相交于A,B两点. 用
的直线与抛物线相交于A,B两点. 用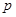 表示A,B之间的距离;
表示A,B之间的距离;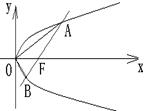
 的直线与抛物线相交于A,B两点.用p表示A,B之间的距离.
的直线与抛物线相交于A,B两点.用p表示A,B之间的距离.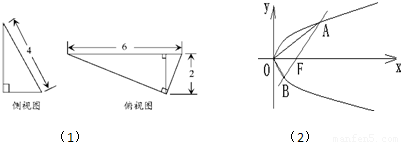
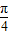 的直线与抛物线相交于A,B两点.用p表示A,B之间的距离.
的直线与抛物线相交于A,B两点.用p表示A,B之间的距离.