题目内容
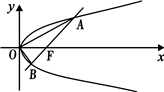 过直角坐标平面xOy中的抛物线y2=2px(p>0)的焦点F作一条倾斜角为
过直角坐标平面xOy中的抛物线y2=2px(p>0)的焦点F作一条倾斜角为| π | 4 |
(1)求直线AB的方程;
(2)试用p表示A、B之间的距离;
(3)当p=2时,求∠AOB的余弦值.
参考公式:(xA2+yA2)(xB2+yB2)=xAxB[xAxB+2p(xA+xB)+4p2].
分析:(1)根据所给的抛物线的方程写出抛物线的焦点坐标,又有所给的直线的倾斜角得到这条直线的斜率,由点斜式写出直线的方程,整理成最简形式.
(2)要求两点之间的距离,首先要把直线与抛物线方程联立,整理出关于x的方程,根据根和系数之间的关系,和抛物线的定义,写出结果.
(3)根据所给的p的值,写出具体的直线的方程,把直线的方程和抛物线方程联立,利用韦达定理,写出根与系数之间的关系,利用余弦定理写出要求的角的余弦值,得到结果.
(2)要求两点之间的距离,首先要把直线与抛物线方程联立,整理出关于x的方程,根据根和系数之间的关系,和抛物线的定义,写出结果.
(3)根据所给的p的值,写出具体的直线的方程,把直线的方程和抛物线方程联立,利用韦达定理,写出根与系数之间的关系,利用余弦定理写出要求的角的余弦值,得到结果.
解答:解:(1)由题意知焦点F(
,0),
∴过抛物线焦点且倾斜角为
的直线方程是y=x-
,
即x-y-
=0,
(2)由
?x2-3px+
=0?xA+xB=3p,xAxB=
?|AB|=xA+xB+p=4p.
(3)由
?x2-6x+1=0?xA+xB=6,xAxB=1.cos∠AOB=
=
=
=
=-
.
∴∠AOB的大小是与p无关的定值.
| p |
| 2 |
∴过抛物线焦点且倾斜角为
| π |
| 4 |
| p |
| 2 |
即x-y-
| p |
| 2 |
(2)由
|
| p2 |
| 4 |
| p2 |
| 4 |
?|AB|=xA+xB+p=4p.
(3)由
|
| |AO|2+|BO|2-|AB|2 |
| 2|AO||BO| |
| xA2+yA2+xB2+yB2-(xA-xB)2-(yA-yB)2 | ||
2
|
| xAxB+yAyB | ||
|
2xAxB-
| ||||
|
3
| ||
| 41 |
∴∠AOB的大小是与p无关的定值.
点评:本题考查直线与圆锥曲线之间的关系,实际上这种问题在解题时考虑的解题方法类似,都需要通过方程联立来解决问题,注意本题中抛物线还有本身的特点,注意使用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
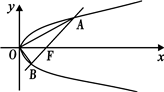 过直角坐标平面xOy中的抛物线y2=2px(p>0)的焦点F作一条倾斜角为
过直角坐标平面xOy中的抛物线y2=2px(p>0)的焦点F作一条倾斜角为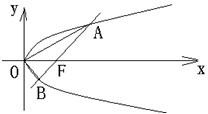 过直角坐标平面xOy中的抛物线y2=2px(p>0)的焦点F作一条倾斜角为
过直角坐标平面xOy中的抛物线y2=2px(p>0)的焦点F作一条倾斜角为
 (2005•上海模拟)本题共有2个小题,第1小题满分8分,第2小题满分6分
(2005•上海模拟)本题共有2个小题,第1小题满分8分,第2小题满分6分