题目内容
(本小题满分14分)如图,在四棱锥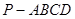 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱 底面ABCD,
底面ABCD, ,E是PC的中点,作
,E是PC的中点,作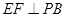 交PB于点F.
交PB于点F.
(I) 证明: PA∥平面EDB;
(II) 证明:PB⊥平面EFD;
(III) 求三棱锥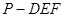 的体积.
的体积.

【答案】
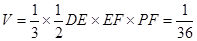
【解析】解:(1)证明:连结AC,AC交BD于O,连结EO
∵底面ABCD是正方形,∴点O是AC的中点
在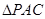 中,EO是中位线,∴PA // EO
中,EO是中位线,∴PA // EO
而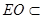 平面EDB且
平面EDB且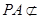 平面EDB,
平面EDB,
所以,PA // 平面EDB. ................4分
(2)证明:∵PD⊥底面ABCD且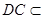 底面ABCD,∴
底面ABCD,∴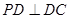
∵PD=DC,可知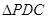 是等腰直角三角形,而DE是斜边PC的中线,
是等腰直角三角形,而DE是斜边PC的中线,
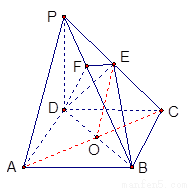 ∴
∴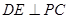 ①
①
同样由PD⊥底面ABCD,得PD⊥BC
∵底面ABCD是正方形,有DC⊥BC,∴BC⊥平面PDC
而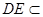 平面PDC,∴
平面PDC,∴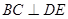 ②
②
由①和②推得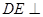 平面PBC
平面PBC
而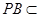 平面PBC,∴
平面PBC,∴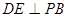
又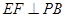 且
且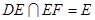 ,所以PB⊥平面EFD
,所以PB⊥平面EFD
.................8分
(3)∵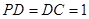 ,
,
由PD⊥平面ABCD,∴ PD⊥BC,
又∵ BC⊥CD,PD∩CD=D,∴BC⊥平面PCD,
∴ BC⊥PC.
在△BDE中,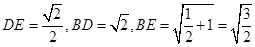 ,
,
∴ 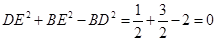 ,即DE⊥BE.
,即DE⊥BE.
而由(2),PB⊥平面EFD,有PB⊥DE,因而DE⊥平面BEF,
在Rt△BPD中,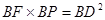 ,
,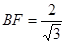 ;Rt△BEF中,
;Rt△BEF中,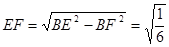 .
.
∴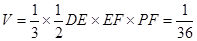 . ........14分
. ........14分

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)