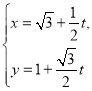题目内容
【题目】已知定点![]() ,圆
,圆![]() ,点
,点![]() 为圆
为圆![]() 上动点,线段
上动点,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,记
,记![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
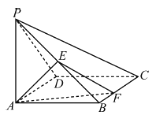
(2)过点![]() 与
与![]() 作平行直线
作平行直线![]() 和
和![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 、
、![]() 和点
和点![]() 、
、![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由中垂线的性质得![]() ,可得出
,可得出![]() ,符合椭圆的定义,可知曲线
,符合椭圆的定义,可知曲线![]() 是以
是以![]() 、
、![]() 为焦点的椭圆,由此可得出曲线
为焦点的椭圆,由此可得出曲线![]() 的方程;
的方程;
(2)设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,将直线
,将直线![]() 的方程与曲线
的方程与曲线![]() 的方程联立,列出韦达定理,利用弦长公式计算出
的方程联立,列出韦达定理,利用弦长公式计算出![]() ,同理得出
,同理得出![]() ,并计算出两平行直线
,并计算出两平行直线![]() 、
、![]() 的距离,可得出四边形
的距离,可得出四边形![]() 的面积关于
的面积关于![]() 的表达式,然后利用双勾函数的单调性可求出四边形
的表达式,然后利用双勾函数的单调性可求出四边形![]() 面积的最大值.
面积的最大值.
(1)由中垂线的性质得![]() ,
,![]() ,
,
所以,动点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆,
的椭圆,
设曲线![]() 的方程为
的方程为![]() ,则
,则![]() ,
,![]() ,
,
因此,曲线![]() 的方程为:
的方程为:![]() ;
;
(2)由题意,可设![]() 的方程为
的方程为![]() ,
,
联立方程得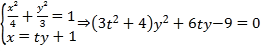 ,
,
设![]() 、
、![]() ,则由根与系数关系有
,则由根与系数关系有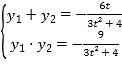 ,
,
所以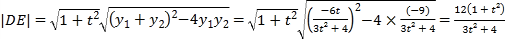 ,
,
同理![]() ,
,![]() 与
与![]() 的距离为
的距离为![]() ,
,
所以,四边形![]() 的面积为
的面积为![]() ,
,
令![]() ,则
,则![]() ,得
,得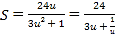 ,
,
由双勾函数的单调性可知,函数![]() 在
在![]() 上为增函数,
上为增函数,
所以,函数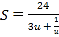 在
在![]() 上为减函数,
上为减函数,
当且仅当![]() ,即
,即![]() 时,四边形
时,四边形![]() 的面积取最大值为
的面积取最大值为![]() .
.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目