题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为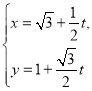 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程及曲线
的极坐标方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 是直线
是直线![]() 上一点,
上一点,![]() 是曲线
是曲线![]() 上一点,求
上一点,求![]() 的最大值.
的最大值.
【答案】(1)![]() ,
,![]() (2)1
(2)1
【解析】
(1)将直线![]() 的参数方程中的参数
的参数方程中的参数![]() 消去,即可得直线
消去,即可得直线![]() 的直角坐标方程,再利用
的直角坐标方程,再利用![]() 可得直线
可得直线![]() 的极坐标方程,曲线
的极坐标方程,曲线![]() 的极坐标方程可变形为
的极坐标方程可变形为![]() ,代入
,代入![]() 可得普通方程;
可得普通方程;
(2)将点![]() ,
,![]() 代入各自曲线的极坐标方程,可得
代入各自曲线的极坐标方程,可得 ,整理得
,整理得![]() ,根据正弦函数的性质可得最值.
,根据正弦函数的性质可得最值.
(1)直线![]() 的参数方程为
的参数方程为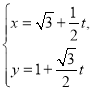 (
(![]() 为参数),
为参数),
转换为直角坐标方程为![]() ,整理得
,整理得![]() ,
,
转换为极坐标方程为![]() .
.
曲线![]() 的极坐标方程为
的极坐标方程为![]() ,整理得
,整理得![]() ,
,
转换为直角坐标方程![]() ,即
,即![]() ;
;
(2)由于![]() 是直线
是直线![]() 上一点,则
上一点,则![]() ,
,![]() 是曲线
是曲线![]() 上一点,则:
上一点,则:![]() ,
,
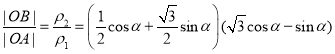
![]()
![]() ,
,
故![]() 的最大值为1.
的最大值为1.

【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式,为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人.第一组工人用第一种生产方式,第二组工人用第二种生产方式,根据工人完成生产任务的工作时间(单位:min)绘制了如图所示的茎叶图:
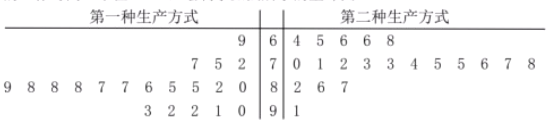
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数,并将完成生产任务所需时间超过和不超过的工人数填入下面的列联表,再根据列联表,能否有99.9%的把握认为两种生产方式的效率有差异?
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
附: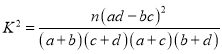 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】某校需从甲、乙两名学生中选一人参加物理竞赛,这两名学生最近5次的物理竞赛模拟成绩如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
学生甲的成绩(分) | 80 | 85 | 71 | 92 | 87 |
学生乙的成绩(分) | 90 | 76 | 75 | 92 | 82 |
(1)根据成绩的稳定性,现从甲、乙两名学生中选出一人参加物理竞赛,你认为选谁比较合适?
(2)若物理竞赛分为初赛和复赛,在初赛中有如下两种答题方案:方案1:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰;方案2:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被淘汰.若学生乙只会5道备选题中的3道,则学生乙选择哪种答题方案进入复赛的可能性更大?